Question

In a class 21 students plays kabaddi, 26 students plays kho-kho and 29 students plays football. Now 14 students play both kabaddi and kho-kho, 12 students play both kabaddi and football, 15 students play both kho-kho and football. If 8 students play all the three games, then find the total no. of students who play kabaddi only?

Answer 1

Hint: We start solving the problem by assigning the variables for the sets that represent the total number of students playing three games. We then follow the standard notation using these variables and write the given information. We then draw Venn diagram and write all the relations which were given in the problem. We use the values, Venn diagrams, and make the necessary calculations required to get the desired result.

Complete step by step answer:
According to the problem, we have given that 21 students play kabaddi, 26 play kho-kho, and 29 students play football. Out of all the students, 14 students play both kabaddi and kho-kho, 12 play both kabaddi and football, 15 play both kho-kho and football. We need to find the total number of students wh plays kabaddi only if 8 students play all the games.
Let us assume that A, B, and C be the sets that students play kabaddi, kho-kho, and football.
As per the information given in the problem we have,
$\Rightarrow n\left( A \right)=21$.
$\Rightarrow n\left( B \right)=26$.
$\Rightarrow n\left( C \right)=29$.
$\Rightarrow n\left( A\cap B \right)=14$.
$\Rightarrow n\left( A\cap C \right)=12$.
$\Rightarrow n\left( B\cap C \right)=15$.
$\Rightarrow n\left( A\cap B\cap C \right)=8$.
Now, let us draw the Venn diagram showing the sets A, B and C.

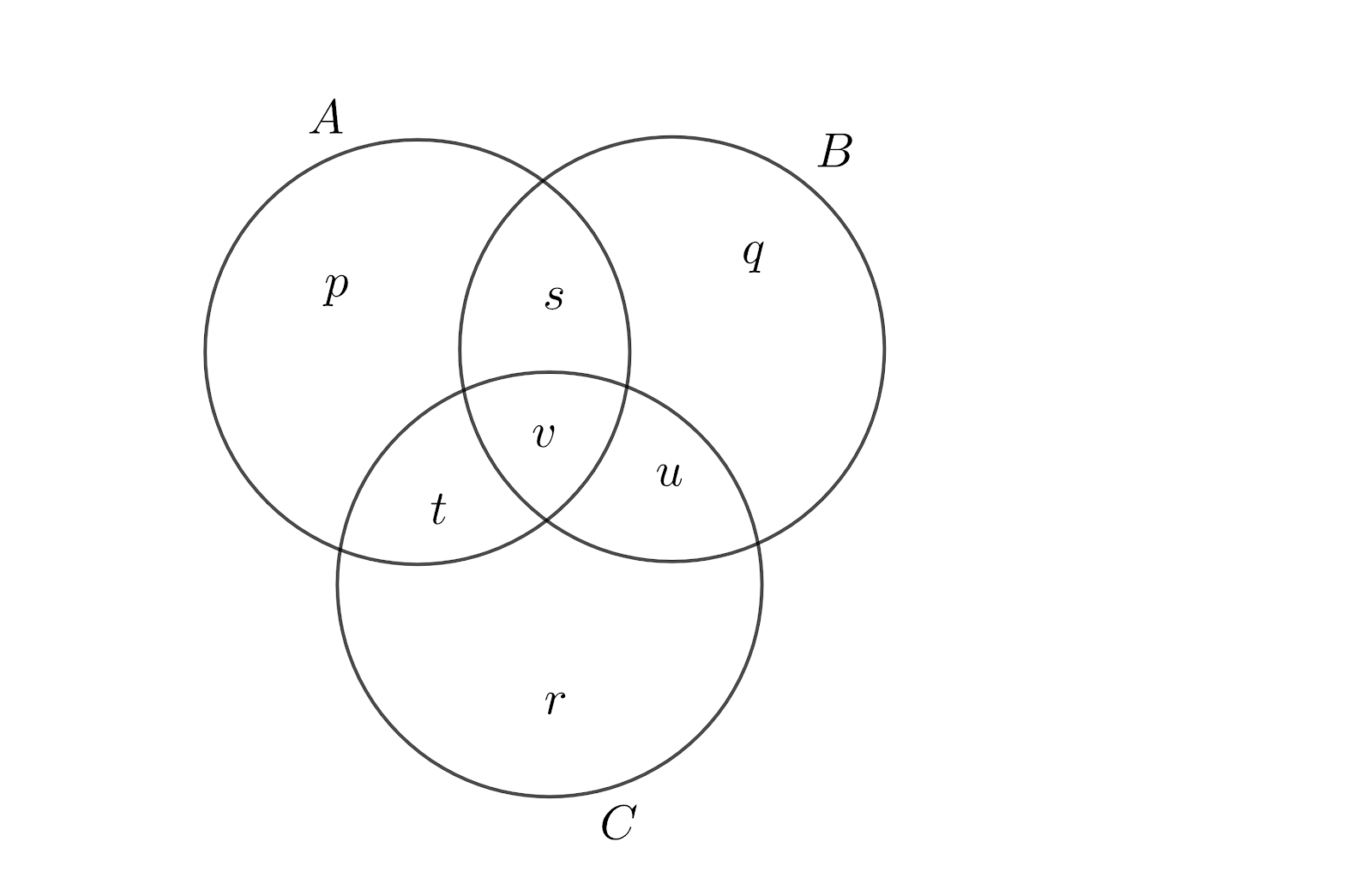
Here p = total number of students who play kabaddi only.
q = total number of students who play kho-kho only.
r = total number of students who play football only.
s = total number of students who play kabaddi and kho-kho but not football.
t = total number of students who play kabaddi and football but not kho-kho.
u = total number of students who play kho-kho and football but not kabaddi.
v = the total number of students who play all three games.
So, we get $n\left( A\cap B\cap C \right)=v=8$, $n\left( A\cap C \right)=t+v=12$, $n\left( A\cap B \right)=s+v=14$ and $n\left( A \right)=p+s+t+v=21$.
Now, $t=12-8=4$.
$s=14-8=6$.
$p=21-6-4-8$.
$p=3$.
So, we have found the number of students who play the only kabaddi is 3.
∴ The total number of students who play kabaddi only is 3.

Note:
Whenever we get this type of problem, we should try to frame the given information in the Venn diagrams as this makes us easy to understand the given information. We should make calculation mistakes for solving this problem. We can also solve this problem without using Venn diagrams but that process can make us commit calculation mistakes and may give confusion. Similarly, we can solve for the total no. of students who play only kho-kho, only football, and any other combination of these three games using the Venn diagram we have just drawn.