Question

In a class 18 students took Physics, 23 students took Chemistry and 24 students took Mathematics of those 13 took both Chemistry and Mathematics, 12 took both Physics and Chemistry and 11 took both Physics and Mathematics. If 6 students offered all the three subjects, find:
i) The total number of students.
ii) How many took Mathematics but not Chemistry.
Iii) How many took exactly one of the three subjects.

Answer 1

Hint: We solve this question by using the basic formulae for sets and their calculations. We are given a set of data which we analyse and calculate the given questions. We draw the Venn diagram required for the question. We calculate the total number of students, the number of students who took Mathematics but not Chemistry and the number of students who took exactly one of the three subjects by using the various formulae for sets.

Complete step by step solution:
In order to solve this question, let us consider the Venn diagram for the given question as given below.

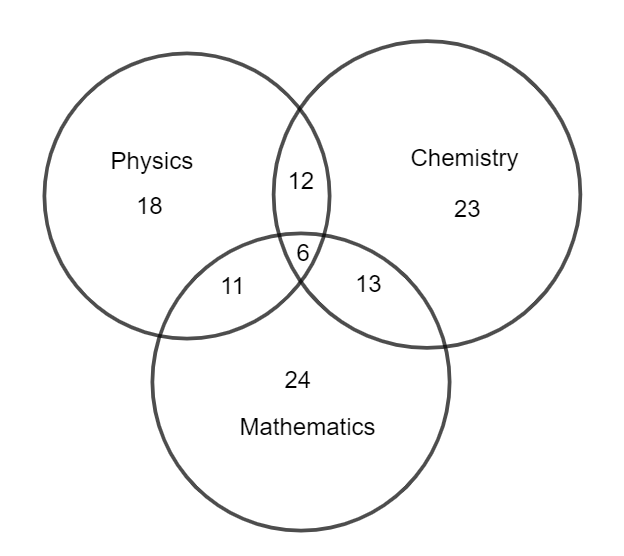
Using this Venn diagram and the basic formulae, we evaluate the question and answer it. We can calculate the total number of students in the class using the formula,
$\Rightarrow n\left( P\bigcup C\bigcup M \right)=n\left( P \right)+n\left( C \right)+n\left( M \right)-n\left( P\bigcap C \right)-n\left( C\bigcap M \right)-n\left( P\bigcap M \right)+n\left( P\bigcap C\bigcap M \right)$
These values can be noted from the Venn diagram or question as $n\left( P \right)=18,n\left( C \right)=23,n\left( M \right)=24,n\left( P\bigcap C \right)=12,n\left( C\bigcap M \right)=13,n\left( P\bigcap M \right)=11,n\left( P\bigcap C\bigcap M \right)=6.$
Using these in the above formula,
$\Rightarrow n\left( P\bigcup C\bigcup M \right)=18+23+24-12-13-11+6$
Adding and subtracting the terms,
$\Rightarrow n\left( P\bigcup C\bigcup M \right)=35$
Hence, the total number of students in the class is 35.
Next, we are required to calculate the number of students who took Mathematics but not Chemistry. We do this by using the set subtraction operation given as,
$\Rightarrow n\left( M-C \right)=n\left( M \right)-n\left( M\bigcap C \right)$
We know the value of $n\left( M \right)=24$ and $n\left( M\bigcap C \right)=13$ , and substituting this in the above formula,
$\Rightarrow n\left( M-C \right)=24-13$
Subtracting the two,
$\Rightarrow n\left( M-C \right)=11$
Hence, the number of students who took Mathematics but not Chemistry is 11.
Next, we are supposed to calculate the number of students who took exactly one of the three subjects. This can be done using the formula,
$\Rightarrow n\left( P \right)+n\left( C \right)+n\left( M \right)-2n\left( P\bigcap C \right)-2n\left( C\bigcap M \right)-2n\left( P\bigcap M \right)+3n\left( P\bigcap C\bigcap M \right)$
Substituting these values from the first part,
$\Rightarrow 18+23+24-2\times 12-2\times 13-2\times 11+3\times 6$
Multiplying and adding the first 3 terms,
$\Rightarrow 65-24-26-22+18$
Adding and subtracting the terms,
$\Rightarrow 83-72=11$
Hence, the number of students who took exactly one of the three subjects is 11.

Note: We need to know the concept of sets in order to solve such problems. We can also solve this question by just using the Venn diagram and calculating the necessary values as per the question. It is important to know how to draw the Venn diagram in such cases.