Question

In a city, three daily newspapers A, B, C are published, 42% read A; 51% read B; 68% read C; 30% read A and B; 28% read B and C; 36% read A and C; 8% do not read any of the three newspapers.
What is the percentage of people who read only one paper?
A) 38%
B) 48%
C) 51%
D) None of the above

Answer 1

Hint: This type question is smoothly solved by Venn diagrams, following some definition and formula we should know before proceeding.
Venn diagrams consist of rectangles and closed curves, usually circles. The universal set is represented by a rectangle and its subsets by a circle.

The notation $n({\text{A}})$ is the numbers of elements of set A
Probabilities are expressed as 0 (impossible) and 1 (certain). This means a probability number is always a number from 0 to 1.
Probability can also be written as a percentage, which is a number from 0 to 100 percent.
Remember section ‘only A’ in Venn diagram means the part of set A except common parts with other sets.

Complete step by step solution:
Step 1: Represent the given information into Venn diagram:

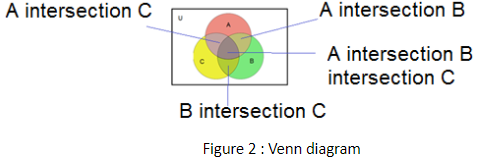
Step 2: define all the sections of Venn diagram according to the given question
Let set A represents people reading newspaper A
Given that % (percentage) of people reading newspaper A = 42%
Hence, Probability (people reading newspaper A) =
                                                                  P(A) $ = \dfrac{{42}}{{100}}$ …… (1)
Let set B represents people reading newspaper B
Given that % (percentage) of people reading newspaper B = 51%
Hence, Probability (people reading newspaper B) =
                                                                  P(B) $ = \dfrac{{51}}{{100}}$ …… (2)
Let set C represents people reading newspaper C
Given that % (percentage) of people reading newspaper C = 68%
Hence, Probability (people reading newspaper C) =
                                                                  P(C) $ = \dfrac{{68}}{{100}}$ …… (3)
Let set $(A \cap B)$ represents people reading newspaper both A and B
Given that % (percentage) of people reading newspaper both A and B = 30%
Hence, Probability (people reading newspaper both A and B) =
                                                                  P($(A \cap B)$) $ = \dfrac{{30}}{{100}}$ ……(4)
Let set $(B \cap C)$ represents people reading newspaper both B and C
Given that % (percentage) of people reading newspaper both B and C = 28%
Hence, Probability (people reading newspaper both B and C) =
                                                                            P($(B \cap C)$) $ = \dfrac{{28}}{{100}}$ …… (5)
Let set $(A \cap C)$ represents people reading newspaper both A and C
Given that % (percentage) of people reading newspaper both A and C = 36%
Hence, Probability (people reading newspaper both A and C) =
                                                                          P($(A \cap C)$) $ = \dfrac{{36}}{{100}}$ …… (6)
Step 3
Set $(A \cup B \cup C)$ represents people reading at least one of the three newspapers A, B and C.
Set $(A \cup B \cup C)'$ represents people who do not read any of the three newspapers A, B and C.
Given that % (percentage) of people do not read any newspaper = 8%
Hence, Probability (people do not read any newspaper) =
                                                                 P($(A \cup B \cup C)'$) $ = \dfrac{8}{{100}}$ …… (7)
Step 4: Find union of Sets A, B, C
Also, P($(A \cup B \cup C)'$) $ = 1 - P((A \cup B \cup C))$
            P($(A \cup B \cup C)$) $ = 1 - P((A \cup B \cup C)')$
                                        $
   = 1 - \dfrac{8}{{100}} \\
   = \dfrac{{100 - 8}}{{100}} \\
 $
                                         $ = \dfrac{{92}}{{100}}$ …… (8)
Step 5:
We know, the number of set of elements in union of set A and set B and set C is given by:
$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(B \cap C) - n(A \cap C) + n(A \cap B \cap C)$ dividing the whole equation by $n( \cup )$, we get
$P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C) - P(A \cap C) + P(A \cap B \cap C)$ …… (9)
As the probability of an event, E is given by:
                                                                        P(E) = $\dfrac{{n(E)}}{{n(S)}}$
Where, $n(E)$is number of element in set E, $n(S)$is number of element in the set S. event E is the subset of sample space S
Step 6: use equation (9) to find the intersection of set A, B and C:
$P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C) - P(A \cap C) + P(A \cap B \cap C)$
$ \Rightarrow \dfrac{{92}}{{100}} = \dfrac{{42}}{{100}} + \dfrac{{51}}{{100}} + \dfrac{{68}}{{100}} - \dfrac{{30}}{{100}} - \dfrac{{28}}{{100}} - \dfrac{{36}}{{100}} + P(A \cap B \cap C)$ (from step (1) to (8))
$
   \Rightarrow {\text{ }}\dfrac{{92}}{{100}} = \dfrac{{161}}{{100}} - \dfrac{{94}}{{100}} + P(A \cap B \cap C) \\
   \Rightarrow {\text{ }}\dfrac{{92}}{{100}} = \dfrac{{67}}{{100}} + P(A \cap B \cap C) \\
   \Rightarrow \dfrac{{92 - 67}}{{100}} = P(A \cap B \cap C) \\
 $
$ \Rightarrow P(A \cap B \cap C) = \dfrac{{25}}{{100}}$ …… (10)
Step 7: find the separate probability of only A, only B, only C, combine them later
Probability of people reading only newspaper A =
$P({\text{reading only A) = }}P(A) - P(A \cap B) - P(A \cap C) + P(A \cap B \cap C)$
                                   $
   = \dfrac{{42}}{{100}} - \dfrac{{30}}{{100}} - \dfrac{{36}}{{100}} + \dfrac{{25}}{{100}} \\
   = \dfrac{{42 - 30 - 36 + 25}}{{100}} \\
 $
                                   $ = \dfrac{1}{{100}}$ …… (11)
Probability of people reading only newspaper B =
$P({\text{reading only B) = }}P(B) - P(A \cap B) - P(B \cap C) + P(A \cap B \cap C)$
                                   $
   = \dfrac{{51}}{{100}} - \dfrac{{30}}{{100}} - \dfrac{{28}}{{100}} + \dfrac{{25}}{{100}} \\
   = \dfrac{{51 - 30 - 28 + 25}}{{100}} \\
 $
                                   $ = \dfrac{{18}}{{100}}$ …… (12)
Probability of people reading only newspaper C =
$P({\text{reading only C) = }}P(C) - P(A \cap C) - P(B \cap C) + P(A \cap B \cap C)$


                                   $
   = \dfrac{{68}}{{100}} - \dfrac{{36}}{{100}} - \dfrac{{28}}{{100}} + \dfrac{{25}}{{100}} \\
   = \dfrac{{68 - 36 - 28 + 25}}{{100}} \\
 $
                                   $ = \dfrac{{29}}{{100}}$ …… (13)
We have subtracted the $P(A \cap B \cap C)$ twice, so it must be added.
Step 8:
Thus,
Probability of people reading only one newspaper =
$
  P({\text{people reading only one newspaper}}) \\
  {\text{ }} = P({\text{reading only A}}) + P({\text{reading only B}}) + P({\text{reading only C}}) \\
 $
                  $
   = \dfrac{1}{{100}} + \dfrac{{18}}{{100}} + \dfrac{{29}}{{100}} \\
   = \dfrac{{1 + 18 + 29}}{{100}} \\
 $ (from step (11) to (13))
                  $ = \dfrac{{48}}{{100}}$ …… (14)
$ \Rightarrow $% (percentage) of people reading only one newspaper = 48%.

Final answer: The percentage of people reading only one newspaper is 48%. The correct option is (B).

Note:
The higher the probability number or percentage of an event, the more likely is it that the event will occur.
Venn diagrams helps to visualize probability of multiple events.
By Venn diagrams, no need to learn the formula of relation between union and intersection of sets. You can simply derive it by looking at the diagram.
For example: $\left( {A \cup B} \right)$means all the elements of set A as well as set B

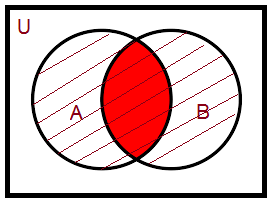
 Figure: $\left( {A \cup B} \right)$[shaded portion]

From the Venn diagram, we can easily infer that:
$n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) - n\left( {A \cap B} \right)$
Here, we have subtracted the $n(A \cap B)$ twice, so it must be added.