Question

In a circus, a stuntman rides a motorbike in a circular track of radius \[R\] in the vertical plane. The minimum speed at highest point of track will be:
(A). \[\sqrt {2gR} \]
(B). \[2gR\]
(C). \[\sqrt {3gR} \]
(D). \[\sqrt {gR} \]

Answer 1

- Hint: You can start by defining the concept of net forces. Then describe what forces affect the body at the highest point of the race track. Then use the equation \[{F_{net}} = mg - {F_N}\] and \[{a_c} = \dfrac{{{v^2}}}{R}\] to find the speed of the body at the highest point of race track.

Complete step-by-step solution -
The diagram for the given problem is

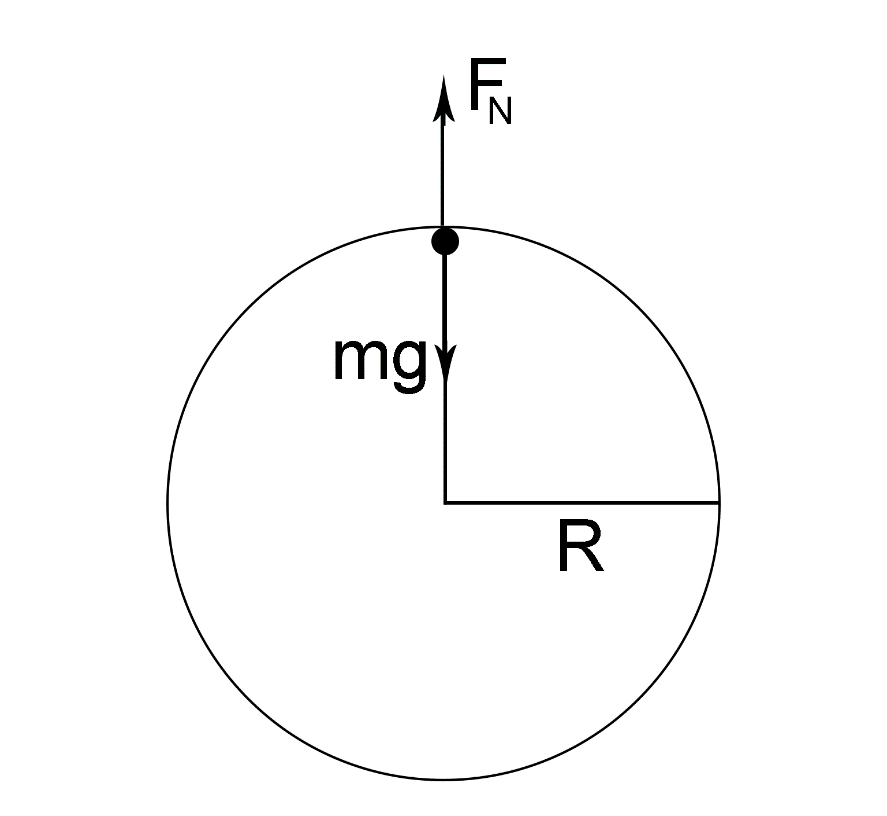
To solve this problem, we have to remember the concept of net forces.
The bikes and the motorbike together can be considered as a single body. A body applies a normal force\[({F_N})\] on every surface it is in contact with and it also receives a reverse normal force\[({F_N})\] back. In this problem we are required to calculate the minimum velocity of the body at the highest point of the circular track. On the highest point, when the bike has minimum velocity the centrifugal acceleration only opposes the gravitational acceleration, so normal forces become zero.
Let \[{F_{net}} = \]net force on the bike and biker
\[{F_{mg}} = \]Force due to gravity on the body
\[{F_N} = \]Normal force
\[v = \]Velocity of the body at the highest point on the race track
\[{a_c} = \]Centrifugal acceleration
Given \[Radius = R\]
At any point of the race track
\[{F_{net}} = mg - {F_N}\]
At the highest point of the race track, \[{F_N} = 0\]
\[{F_{net}} = mg\](Equation 1)
By using \[{2^{nd}}\]law of Newton, we know
\[{F_{net}} = m{a_c}\](Equation 2)
Comparing equation 1 and equation 2
\[m{a_c} = mg\](Equation 3)
We also know\[{a_c} = \dfrac{{{v^2}}}{R}\] . Substituting this value in equation 3
\[m * \dfrac{{{v^2}}}{R} = mg\]
\[{v^2} = Rg\]
\[v = \sqrt {Rg} \]
So, the minimum speed of the body at the highest point of the race track is\[\sqrt {Rg} \].
Hence, option D is the correct choice.

Note: To solve this problem, we also used the concept of the centrifugal force is an inertial force that acts on a body that moves in a curved path or circular path. Centrifugal force is considered the opposite of centripetal force. For a body in circular path, the centripetal force is towards the inner side and the centrifugal force is towards the outer side of the circular path.