Question

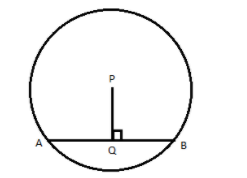
In a circle with centre P, chord AB is drawn of length 15cm.${\text{Seg}}\,PQ\,\, \bot \,\,{\text{chord}}\,AB$, then find $l\left( {QB} \right)$

Answer 1

Hint: From the figure, we can conclude that the PQ is the perpendicular radius drawn to the chord AB. Then we can say that Q is the midpoint of AB by the properties of the circle. Then we can find the required length QB by taking the half of the length of AB.

Complete step-by-step answer:
We have a circle with centre P. AB is a chord of the circle. It is given that the length of AB is 15cm.
PQ is the perpendicular from the centre P to the chord AB. We know that the radius perpendicular to the chord is the perpendicular bisector of the chord. From the figure, PQ is the part of a radius that is perpendicular to the chord AB. So, PQ is the bisector of the chord AB. In other words, we can say that Q is the midpoint of AB and hence Q divides AB into 2 equal parts
 $ \Rightarrow AB = AQ + QB$
As Q is the midpoint, we can write, $QB = AQ$
 $ \Rightarrow AB = 2QB$
On dividing throughout with 2, we get,
$ \Rightarrow QB = \dfrac{{AB}}{2}$
We are given that AB is 15 cm
$ \Rightarrow QB = \dfrac{{15}}{2}$
After division we get,
$ \Rightarrow QB = 7.5$
Therefore, $l\left( {QB} \right) = 7.5cm$

Note: A circle is the collection of all the points that are at constant distance from a fixed point. The fixed point is called the centre of the circle and the constant distance is called the radius. A chord is the line segment which connects any 2 points on the circle. The largest chord is the diameter. It has a length of twice the radius of the circle and passes through the centre. The radius drawn perpendicular to the chord bisects the chord.