Question

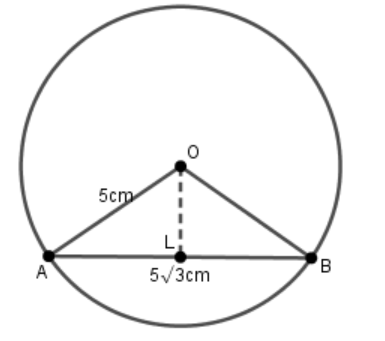
In a circle with centre O and radius $5cm$, AB is a chord of length $5\sqrt 3 cm$. Find the area of sector AOB.

A). $\dfrac{{25\pi }}{2}c{m^2}$
B). $\dfrac{{23\pi }}{3}c{m^2}$
C). $\dfrac{{25\pi }}{7}c{m^2}$
D). None of these

Answer 1

Hint: We are given a circle and we need to find the area of the sector of the circle i.e. we need to find the area of AOB. We know the area of the sector = $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$. Where $\theta $ is an angle subtended at centre and $\pi {r^2}$ is the area of a circle. To find the area of a sector, first we have to find the angle subtended at the centre and then we will find the area of the sector.
Formulas used:
Area of the sector = $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$.

Complete step-by-step solution:
Given, Radius of the circle = $5cm$ and length of chord = $5\sqrt 3 cm$
To find angle subtended at centre:
As we know $AB = 5\sqrt 3 cm$
$\therefore AL = \dfrac{{5\sqrt 3 }}{2}$ (If a radius of a circle is perpendicular to a chord in the circle, then the radius bisects the chord )
In $\vartriangle OLA$, we have
Let $\angle AOL = \theta $
$\therefore \sin \theta = \dfrac{{AL}}{{OA}}$ (As we know $\sin \theta = \dfrac{{\operatorname{P} erpendicular}}{{Hypotenuse}}$)
Substitute the values of $AL$ and $OA$.
$ \Rightarrow \sin \theta = \dfrac{{\dfrac{{5\sqrt 3 }}{2}}}{5}$
It can also be written as,
$ \Rightarrow \sin \theta = \dfrac{{5\sqrt 3 }}{2} \times \dfrac{1}{5}$
On cancelling, we get
$ \Rightarrow \sin \theta = \dfrac{{\sqrt 3 }}{2}$
$ \Rightarrow \sin \theta = \sin 60^\circ $
$\therefore \theta = 60^\circ $
$\angle AOL + \angle BOL = \angle AOB$ (In $\vartriangle OLA$ and $\vartriangle OLB$, $\angle AOL = \angle BOL$ because both triangles have one common side, one angle of $90^\circ $ and one side of equal length. Therefore, by SAS property both triangles are congruent )
$60^\circ + 60^\circ = \angle AOB$
$ \Rightarrow \angle AOB = 120^\circ $
Now, we will find the area of the sector AOB.
Area of the sector = $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$.
Substitute the values of $\theta $ and radius in the above-written formula.
Area of the sector = $\dfrac{{120^\circ }}{{360^\circ }} \times \pi \times {5^2}c{m^2}$
On simplifying, we get
Area of the sector = $\dfrac{1}{3} \times 25\pi c{m^2}$
Therefore, area of the sector = $\dfrac{{25\pi }}{3}c{m^2}$. Hence option D is the correct option.

Note: There are lots of variations of this question but the core concept is the same. We’ll be having some values, and then we need to use the correct formula to get the value. Students should be careful about the unit. Take care of the calculations so as to be sure of the final answer. Here we should know the difference between sector and segment of a circle, then use the formula accordingly, else a minor mistake can make the answer completely wrong.