Question

In a circle of radius 4.5cm draw two radii such that the angle between them is $70{}^\circ $. Construct tangents at non-centre ends of the radii.

Answer 1

Hint: Draw a circle of radius 4.5cm. Now drawn any radius of the circle and draw an angle of measure $70{}^\circ $ with the radius drawn. Hence draw the radius making an angle of $70{}^\circ $ with the previously drawn radius. Now draw two perpendicular lines to these two radii at non-centre points. Hence draw two tangents to the circle.

Complete step by step solution:
Steps of construction:
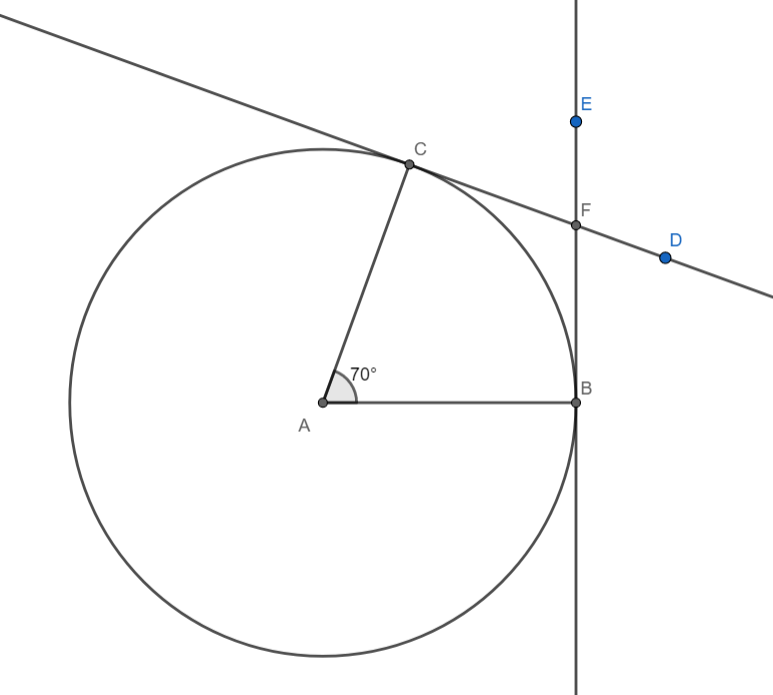
[1] Mark point A on paper. With A as centre and radius, AB = 4.5cm draw a circle.

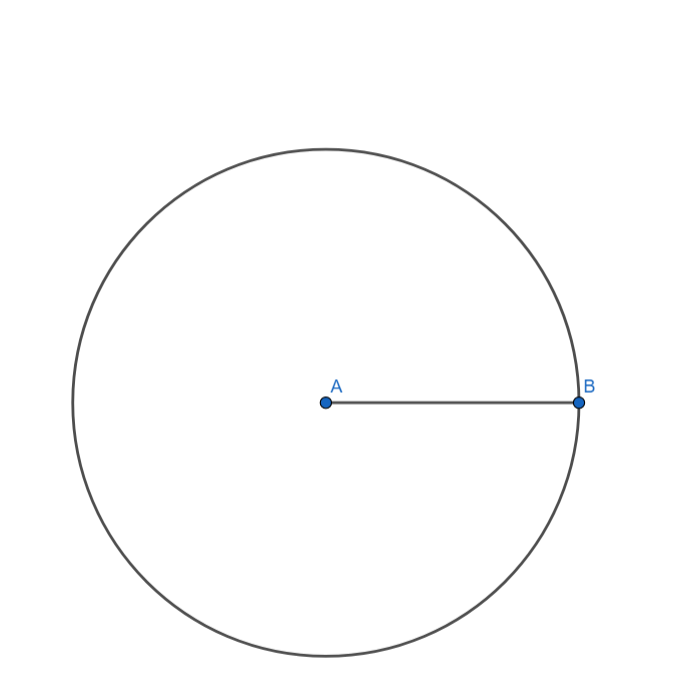
[2] On the line segment AB draws an angle CAB $70{}^\circ $.

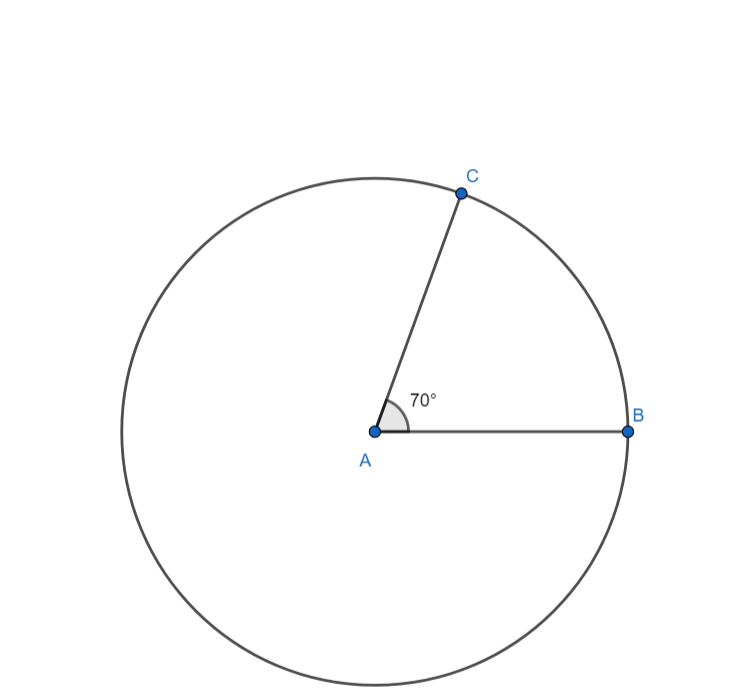
[3] CA and AB are the radii of the circle at an angle of $70{}^\circ $ with each other.
[4] Through C draw a line DC perpendicular to the radius AC.

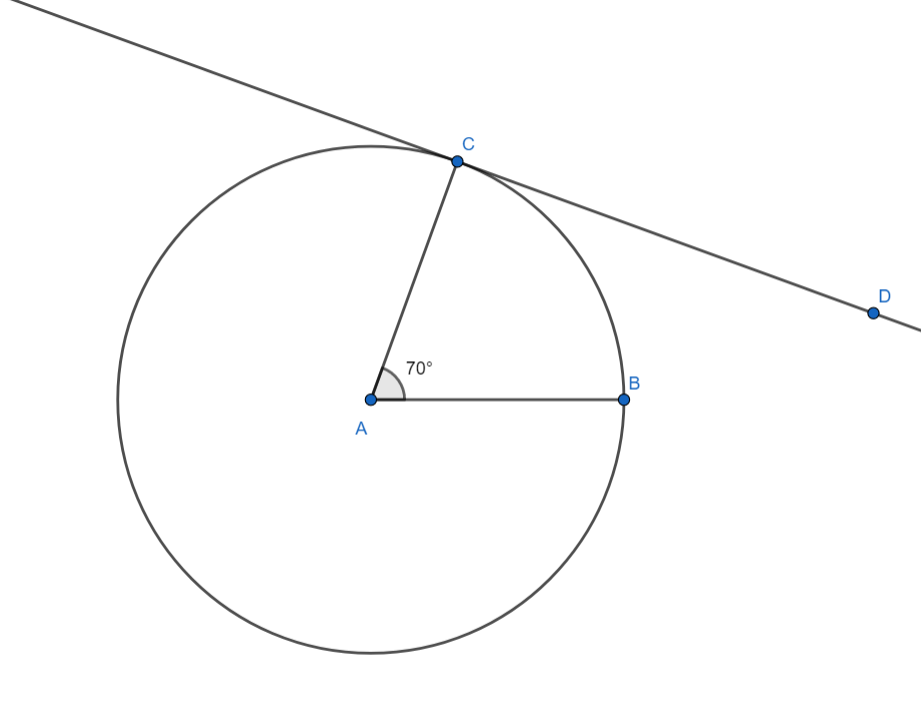
[5] Through B draw a line BE perpendicular to the radius AB

[6] Hence the lines DC and EB are the required tangents to the circle

Note: Justification of Construction:
We know that the tangent to a circle and the radius of a circle are perpendicular to each other at the point of contact.
Since AC and DC are perpendicular to each other and AC is the radius of the circle and C the point of contact, DC is a tangent to the circle.
Since AB and EB are perpendicular to each other, and AB is the radius of the circle and B the point of contact, EB is a tangent to the circle.
Hence EB and DC are tangents to the circle on the non-centric points of radii which are at an angle of $70{}^\circ $ with each other.
Verification of correctness of the construction:
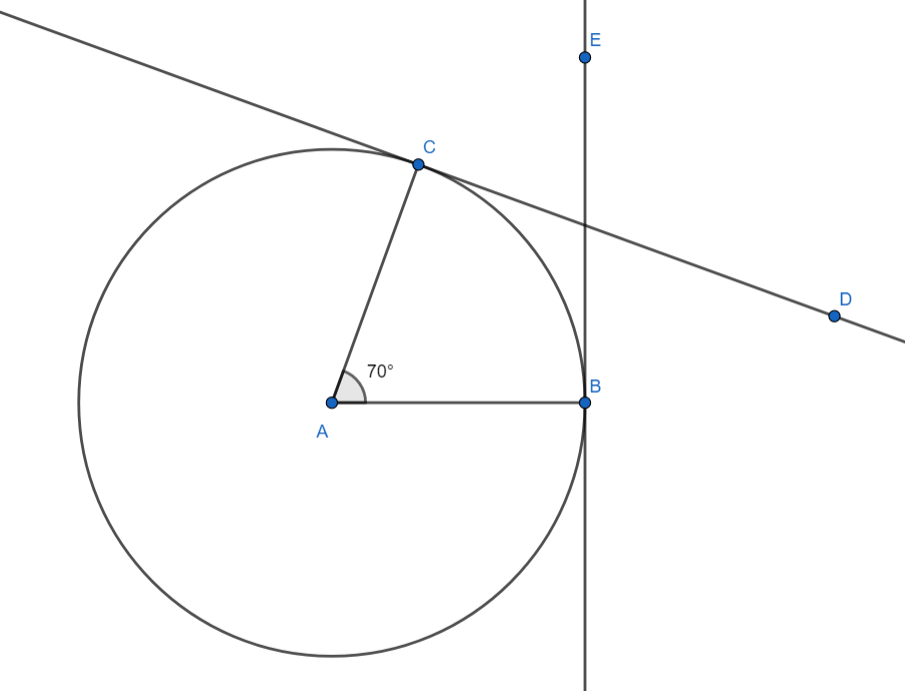
We know that the points of contact, the centre of the circle and the point of intersection of tangents are concyclic with the midpoint of the line joining the point of intersection of the tangents with the centre as the centre of the circle. Hence draw a perpendicular bisector of the line segment FA and let it intersect FA at G. With G as centre and radius GA draw a circle and verify it passes through all points A,B,C and F.

Hence our construction is verified to be correct.