Question

In a circle of 5 feet radius, what is the length of the arc which subtends an angle of ${{33}^{\text{o}}}15'$ at the centre?

Answer 1

Hint: We will apply the formula to find the length of an arc. The formula is given by $L=\dfrac{\theta }{{{360}^{\text{o}}}}\times 2\pi R$, where R is the radius of the circle and $\theta $ is the angle that is measured for the arc of the circle.

Complete step-by-step answer:
The required diagram for the question is shown below.

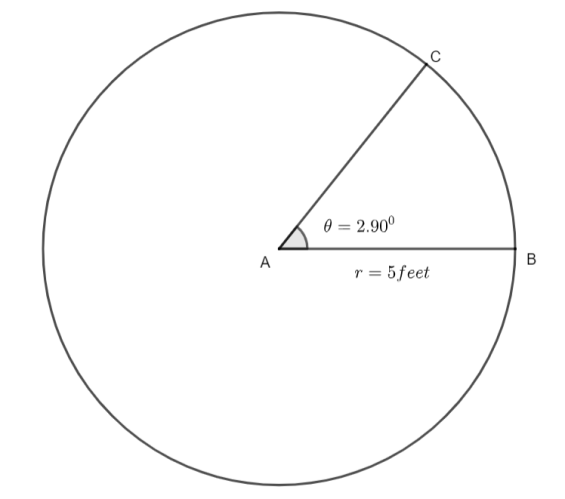
Now, first we consider the angle which is given to us as ${{33}^{\text{o}}}15'$. Here, we will apply the formula to convert minutes into degrees as ${{\left( 1 \right)}^{\text{o}}}=60'$ or 1 minute is divided into 1 by 60 degrees. Numerically, this is represented as $\left( 1 \right)'={{\left( \dfrac{1}{60} \right)}^{\text{o}}}$. As we can write ${{33}^{\text{o}}}15'$ as ${{33}^{\text{o}}}15'={{33}^{\text{o}}}+15'$. Therefore, after substituting the $\left( 1 \right)'={{\left( \dfrac{1}{60} \right)}^{\text{o}}}$ in ${{33}^{\text{o}}}15'={{33}^{\text{o}}}+15'$ we will have,
$\begin{align}
  & {{33}^{\text{o}}}15'={{33}^{\text{o}}}+15' \\
 & \Rightarrow {{33}^{\text{o}}}15'={{33}^{\text{o}}}+{{\left( 15\times \dfrac{1}{60} \right)}^{\text{o}}} \\
 & \Rightarrow {{33}^{\text{o}}}15'={{\left( 33+\dfrac{15}{60} \right)}^{\text{o}}} \\
 & \Rightarrow {{33}^{\text{o}}}15'={{\left( \dfrac{1980+15}{60} \right)}^{\text{o}}} \\
 & \Rightarrow {{33}^{\text{o}}}15'={{\left( \dfrac{1995}{60} \right)}^{\text{o}}} \\
 & \Rightarrow {{33}^{\text{o}}}15'={{\left( \dfrac{133}{4} \right)}^{\text{o}}} \\
\end{align}$
Now, we have degree of the circle as $\theta ={{\left( \dfrac{133}{4} \right)}^{\text{o}}}$ and we are already given the value of radius of the circle as R = 5 feet. Therefore, we can now apply the formula to find the length of an arc. The formula is given by $L=\dfrac{\theta }{{{360}^{\text{o}}}}\times 2\pi R$, where R is the radius of the circle and $\theta $ is the angle that is measured for the arc of the circle.
Therefore, the length of the arc is given by,
$\begin{align}
  & L=\dfrac{\theta }{{{360}^{\text{o}}}}\times 2\pi R \\
 & \Rightarrow L=\dfrac{{{\left( \dfrac{133}{4} \right)}^{\text{o}}}}{{{360}^{\text{o}}}}\times 2\pi 5 \\
 & \Rightarrow L=\dfrac{{{\left( 133 \right)}^{\text{o}}}}{{{360}^{\text{o}}}\times {{4}^{\text{o}}}}\times 2\pi 5 \\
 & \Rightarrow L=\dfrac{133}{72\times 2}\times \pi \\
 & \Rightarrow L=\dfrac{133}{144}\times \pi \\
 & \Rightarrow L=\dfrac{133}{144}\pi \\
\end{align}$
After this we will substitute $\pi =\dfrac{22}{7}$ in $L=\dfrac{133}{144}\pi $. Therefore, we get
$\begin{align}
  & L=\dfrac{133}{144}\pi \\
 & \Rightarrow L=\dfrac{133}{144}\times \dfrac{22}{7} \\
 & \Rightarrow L=\dfrac{19}{72}\times \dfrac{11}{1} \\
 & \Rightarrow L=\dfrac{209}{72} \\
\end{align}$
Hence, the length of the arc of the circle is given by $L=\dfrac{209}{72}$.

Note: If we don’t want our answer in fraction then we will not stop with $L=\dfrac{209}{72}$. We will convert it into decimals after dividing the numerator by denominator. Thus, we get $L=2.90$ which is an approximate value. We could have also substituted $\pi =3.14$ instead of $\pi =\dfrac{22}{7}$ in $L=\dfrac{133}{144}\pi $. Therefore, we get
$\begin{align}
  & L=\dfrac{133}{144}\pi \\
 & \Rightarrow L=\dfrac{133}{144}\times 3.14 \\
 & \Rightarrow L=0.92\times 3.14 \\
 & \Rightarrow L=2.8888 \\
\end{align}$