Question

In a charged spherical conductor of radius $10\,cm$ has a potential $V$ from its center, then the potential at a point $15\,cm$ away from the center will be then
A. $3V$
B. $\dfrac{3}{2}V$
C. $\dfrac{2}{3}V$
D. $\dfrac{1}{3}V$

Answer 1

Hint: Here, we will calculate the potential both at a distance of $10\,cm$ and $15\,cm$ from the center of the sphere. We will divide both the potentials to calculate the potential at a distance of $15\,cm$ from the center of the sphere. Here, we will take the potential that $15\,cm$ away from the sphere as $V'$ .

Formula used:
The formula used for calculating potential at any point is given by
$V = \dfrac{{kQ}}{R}$
Where, $V$ is the potential, $k$ is the coulomb’s constant, $Q$ is the charge, and $R$ is the distance of the charge from any point.

Complete step by step answer:
Consider a spherical conductor of radius $10\,cm$ having a potential $V$ at a distance of $10\,cm$ from the center, which is as shown below

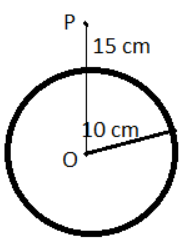
Here, $P$ is the point at a distance of $15\,cm$ from the center where the electric potential $V$ is to be calculated.
Therefore, the radius of the sphere, $R = 10\,cm$
The distance of the point $P$ from the center, $r = 15\,cm$
Now, potential $V$ can be calculated by using the following formula
$V = \dfrac{{kQ}}{R}$
Therefore, the potential $V$ from the center of the sphere is given by
$V = \dfrac{{kQ}}{R}$
$ \Rightarrow \,V = \dfrac{{kQ}}{{10}}$
Now, the potential at the point $P$ will be taken as $V'$ . therefore, the potential at a distance $r$ is given by
$V' = \dfrac{{kQ}}{r}$
$ \Rightarrow \,V' = \dfrac{{kQ}}{{15}}$
Now, dividing $V$ by $V'$ , we get
$\dfrac{V}{{V'}} = \dfrac{{\dfrac{{kQ}}{{10}}}}{{\dfrac{{kQ}}{{15}}}}$
$\dfrac{V}{{V'}} = \dfrac{{kQ}}{{10}} \times \dfrac{{15}}{{kQ}}$
$ \Rightarrow \,\dfrac{V}{{V'}} = \dfrac{{15}}{{10}}$
$ \Rightarrow \,\dfrac{V}{{V'}} = \dfrac{3}{2}$
$ \Rightarrow \,V' = \dfrac{2}{3}V$
Therefore, the potential at a point $15\,cm$ away from the center of the sphere is $\dfrac{2}{3}V$.
Hence, option (C) is the correct option.

So, the correct answer is “Option C”.

Note:
The terms potential and Electric potential are different from each other. Potential is defined as the ability of an object to do something. On the other hand, an electric potential is defined as the amount of work done that is needed to displace a charge from the reference point to a specific point without producing any acceleration.