Question

In a certain group of 75 students, 16 students are taking physics, Geography and English, 24 students are taking Physics and Geography, 30 students are taking Physics and English and 22 students are taking Geography and English. However, 7 students are taking only Physics, 10 students are taking only Geography and 5 students are taking only English. How many of these students are taking Physics?
(a) n(P) = 45
(b) n(P) = 35
(c) n(P) = 65
(d) n(P) = 55

Answer 1

Hint: Here, we will first draw the Venn diagram where three circles will represent the number of students in the three subjects and the union set will represent the total number of students in the group. After that, we will find the total number of students belonging to each region of the Venn diagram and hence calculate the number of students taking Physics using the given data.

Complete step-by-step answer:
The Venn diagram for the given case can be drawn as:

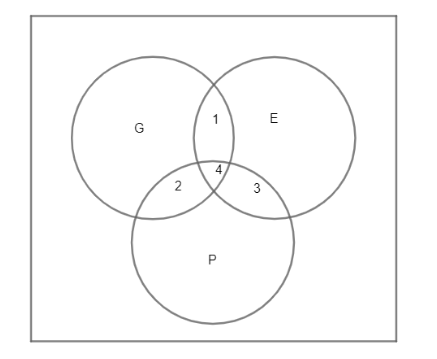
Here, region 1 represents $ G\cap E $ which means students studying both Geography and English.
Region 2 represents $ G\cap P $ which means students studying Geography and Physics.
Region 3 represents $ E\cap P $ which means students studying English and Physics.
Region 4 represents $ G\cap P\cap E $ which means students studying Geography, Physics as well as English.
We know that the region common between P and E gives $ P\cap E $ which is equal to the number of students studying Physics and English.
Similarly, $ P\cap G $ = number of students studying Physics and geography.
And, \[P\cap G\cap E\] = number of students studying Physics, English as well as geography.
Now, it is given that there are 7 students who study only physics. So, number of students studying physics is given as:
 $ n\left( P \right)=7+n\left( P\cap E \right)+n\left( P\cap G \right)-n\left( P\cap G\cap E \right)........\left( 1 \right) $
We have to subtract $ n\left( P\cap G\cap E \right) $ because $ P\cap E $ as well as $ P\cap G $ contains the region of intersection of P, E and G and hence it is counted twice. So, we have to subtract it.
Since, $ n\left( P\cap E \right) $ = 30, V = 24 and $ n\left( P\cap G\cap E \right) $ = 16.
On putting these respective values in equation (1), we get:
n(P) = 7+30+24 – 16
Or, n(P) = 61 – 16 = 45
Hence, option (a) is the correct answer.

Note: Students should keep in mind that $ n\left( P\cap G\cap E \right) $ has to be subtracted from the sum of $ n\left( P\cap G \right) $ and $ n\left( P\cap E \right) $ otherwise it will lead to incorrect answer. This is necessary because the region $ P\cap G\cap E $ comes under both the regions, that is, $ P\cap G\cap E $ is included in $ P\cap G $ as well as in $ P\cap E $ . So, when $ P\cap G $ and $ P\cap E $ are added, $ P\cap G\cap E $ gets added twice. All the calculations must be done properly to avoid mistakes.