Question

In a Carnot's cycle, the working substance absorbs heat ${Q_1}$ at temperature ${T_1}$ and rejects heat ${Q_2}$ at temperature ${T_2}$ . The change of entropy during Carnot's cycle is:
A. $\dfrac{{{Q_1}}}{{{T_1}}}$
B. $\dfrac{{{Q_2}}}{{{T_2}}}$
C. $\dfrac{{{Q_1}}}{{{T_1}}} + \dfrac{{{Q_2}}}{{{T_2}}}$
D. Zero

Answer 1

Hint: This question is based on the Carnot cycle. You need to find the entropy for all the four processes of the cycle in order to calculate the entropy for the whole cycle.

Complete step by step answer:
 The Carnot cycle is an ideal reversible cycle, and it has four reversible processes. The four processes constitute a Carnot cycle, i.e. constant temperature heat addition, isentropic expansion, constant temperature heat rejection and isentropic compression.
The entropy change expression is given by $\Delta S = \dfrac{Q}{T}$
Where Q is the heat interaction in the process, and T is the temperature of the process.

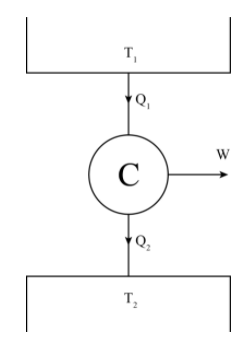
The Carnot cycle has only two processes where heat interaction is taking place, i.e. constant temperature heat addition and constant temperature heat rejection.
For constant temperature heat addition at the temperature the entropy change is $\Delta {S_1} = \dfrac{{{Q_1}}}{{{T_1}}}$
For constant temperature heat rejection at the temperature the entropy change is $\Delta {S_2} = - \dfrac{{{Q_2}}}{{{T_2}}}$
Since the Carnot cycle is reversible so, $\dfrac{{{Q_1}}}{{{T_1}}} = \dfrac{{{Q_2}}}{{{T_2}}}$
Then the total entropy change for the cycle is,
$\begin{array}{c}
\Delta S = \dfrac{{{Q_1}}}{{{T_1}}} - \dfrac{{{Q_2}}}{{{T_2}}}\\
\Rightarrow \Delta S = 0
\end{array}$
Hence, the entropy change for the Carnot cycle is zero. Since the Carnot cycle is an ideal cycle, and the entropy change is zero here, it is the most suitable heat engine cycle. The efficiency of the Carnot cycle is thus having the highest efficiency of all the cycles. But it is not practically possible. In practical cycles, the entropy change is never zero because we can't have all the processes reversible.

So, the correct answer is “Option D”.

Note:
In thermodynamics, the entropy change is always related to heat and temperature, so you may go wrong in this question in analyzing the heat interaction in the particular process.
The efficiency of the Carnot cycle is thus having the highest efficiency of all the cycles.