Question

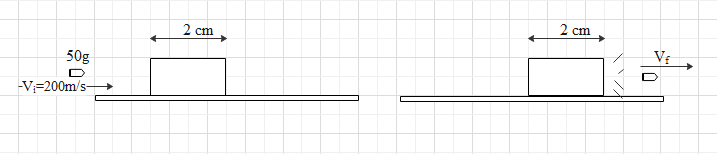
In a ballistic demonstration a police officer fires a bullet of mass \[50g\] with speed \[200m{{s}^{-1}}\] on soft plywood of thickness \[2cm\]. The bullet emerges with only \[10\%\] of its initial kinetic energy. The emergent speed of the bullet is:
(A)\[2\sqrt{10}m{{s}^{-1}}\]
(B)\[20\sqrt{10}m{{s}^{-1}}\]
(C)\[10\sqrt{2}m{{s}^{-1}}\]
(D)\[10\sqrt{20}m{{s}^{-1}}\]

Answer 1

Hint: Here initial speed and final speed are given; also the mass of the bullet is given. In this case, initial kinetic energy and final kinetic energy can be calculated from the given data. After those two equations are generated and solving them leads to the solution of this sum.

Formula used:
\[K=\dfrac{1}{2}m{{v}^{2}}\]

Complete answer:
In this question given that,
Mass of the bullet \[{{m}_{b}}=50g=50\times {{10}^{-3}}kg\]
Initial speed of the bullet \[{{v}_{i}}=200m{{s}^{-1}}\]
Final speed of the bullet \[{{v}_{f}}\text{ }m{{s}^{-1}}\]

Now we have to find the initial and final energy of the bullet.
For initial kinetic energy of bullet;
\[{{K}_{i}}=\dfrac{1}{2}{{m}_{b}}{{v}_{i}}^{2}\]
\[\therefore {{K}_{i}}=\dfrac{1}{2}\times (50\times {{10}^{-3}})\times {{(200)}^{2}}\]
\[\therefore {{K}_{i}}=1000\text{ }kg\text{ }m{{s}^{-1}}\]

For final kinetic energy of bullet;
\[{{K}_{f}}=\dfrac{1}{2}{{m}_{b}}{{v}_{f}}^{2}\]
\[\therefore {{K}_{f}}=\dfrac{1}{2}\times (50\times {{10}^{-3}})\times {{v}_{f}}^{2}\] \[.....(1)\]

But in question given that;
\[\Rightarrow {{K}_{f}}=10\%\] of \[{{K}_{i}}\]
\[\Rightarrow {{K}_{f}}=\dfrac{10}{100}\times 1000\] \[.....(2)\]
Equating both the equations \[(1)\]and\[(2)\],
\[\Rightarrow \dfrac{1}{2}\times (50\times {{10}^{-3}})\times {{v}_{f}}^{2}=\dfrac{10}{100}\times 1000\]
\[\Rightarrow {{v}_{f}}^{2}=\dfrac{100\times 2}{50\times {{10}^{-3}}}\]
\[\Rightarrow {{v}_{f}}^{2}=4000\]
\[\Rightarrow {{v}_{f}}=20\sqrt{10}\text{ m}{{\text{s}}^{-1}}\]

So, the correct answer is “Option B”.

Additional Information:
The kinetic energy of the particle is dependent on how much force is given to the particle and because of that how much speed the particle will gain. Kinetic energy also depends on the mass of the particle. In all cases to conserve the momentum of the system, if the body has less mass comparatively another part of the system it has high speed and high kinetic energy. In this particular question, kinetic energy plays a very important role. In mechanics total energy of the system is conserved but in the case of a particular energy, it may not be conserved.

Note:
The energy conservation law is not applicable here because final energy is \[10\%\] of initial energy so \[90%\] of energy lost during bullet and plywood collision. So it is better to not use energy conservation law if only one form of energy is given and another form is not present.