Question

If T be the period of revolution of a planet revolving around sun in an orbit of mean radius R, then identify the correct graph from the following.

A.

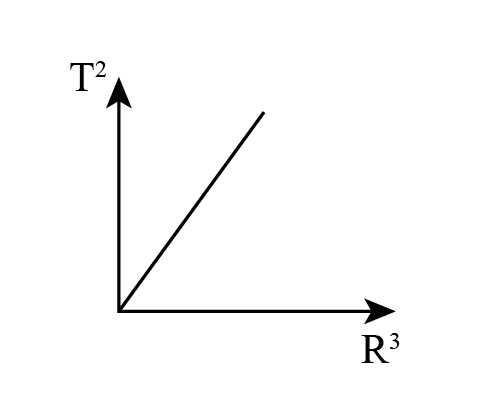
B.

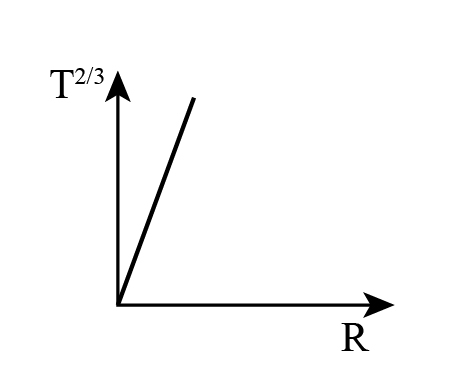
C.

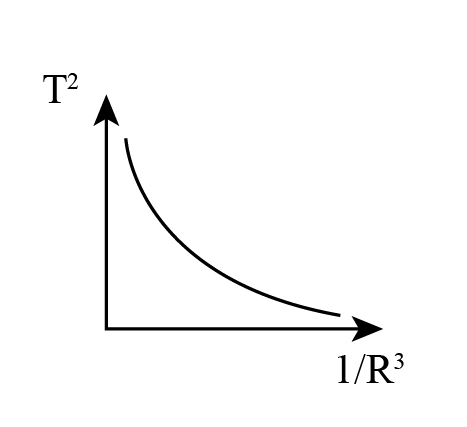
D. None-of these

Answer 1

Hint: The above problem can be resolved using the fundamental relation of Kepler's law. The basic statement for Kepler's law is that when any planet revolves around some orbit then, the square of the time taken by the planet to revolve around the planet will be directly proportional to the radius of the path of orbit, around which the planet is undergoing its revolution. The significance for Kepler's law is that it can draw out the various graphical relations between the period and the radius of circular, which can be determined and analysed using the mathematical relation of Kepler's law.

Complete step by step answer:
The relation between the time period and the radius of the orbit by the Kepler’s law is given as,
\[\begin{array}{l}
{T^2} \propto {R^3}..................\left( 1 \right)\\
R \propto {T^{2/3}}......................\left( 2 \right)\\
{T^2} \propto \dfrac{1}{{1/{R^3}}}........................\left( 3 \right)
\end{array}\]

The above equation 1 represents the graph 1.
The equation 2 represents the graph 2.
And, equation 3 represents graph 3.
Therefore, all the graphs are correct

So, the correct answer is “Option A,B and C”.

Note:
To resolve the given problem, one must understand the concept of Kepler's law. There are basically three statements under the Kepler's law, first of which is that every planet revolving around the orbits, is observed with the sun as the locus. The second statement is that while there is a rotation around the planet, the line joining the planet will swipe the same areas in an equal interval of time. Moreover, the third statements say that the square of the time taken by any planet to revolve according to the orbits is directly proportional to that of the radius of the orbit.