Question

If $z=x+iy$ and if the point P in the Argand Plane represents z, then describe geometrically the locus of z satisfying equations,
$\begin{align}
  & (i)\left| z-2-3i \right|=5 \\
 & \left( ii \right)2\left| z-2 \right|=\left| z-1 \right| \\
\end{align}$

Answer 1

Hint: This question involves the concept of complex number. In this question, we have to put $z=x+iy$ and solve using the concepts like, $z=\left| z \right|=\sqrt{{{x}^{2}}+{{y}^{2}}}$. So, if any complex number is in form of $z=\alpha +i\beta $, then modulus of $\left| z \right|=\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}$.

Complete step-by-step answer:
Now, we will consider the first equation, that is,
$\left| z-2-3i \right|=5$
We have been given in the question that $z=x+iy$, so on substituting this value of z in the above equation, we will get,
$\left| x+iy-2-3i \right|=5$
On writing the real and the imaginary parts separately, we get,
$\left| \left( x-2 \right)+i\left( y-3 \right) \right|=5$
Now, let $\alpha $ be a complex number which is equal to $\left( x-2 \right)+\left( y-3 \right)i$. So, we will get the modulus of $\alpha $ as,
$\left| \alpha \right|=\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}$
So, we can write,
$\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}=5$
On squaring the above equation, we get,
\[{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=25\]
Now, we know that \[{{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}}\] is the equation of a circle with the center $\left( \alpha ,\beta \right)$ and the radius r.
So, on comparing our equation with the equation of the circle, we get to know that,
\[{{\left( x-2 \right)}^{2}}+{{\left( y-3 \right)}^{2}}=25\] is the equation of a circle with the center (2,3) and the radius 5.
So, the locus of z in the equation $\left| z-2-3i \right|=5$ is circle with the center (2,3) and the radius 5.
Now, we will consider the second equation, that is,
$2\left| z-2 \right|=\left| z-1 \right|$
We have been given in the question that, $z=x+iy$, so on substituting this value of z in the above equation, we will get,
$2\left| x+iy-2 \right|=\left| x+iy-1 \right|$
On writing the real and the imaginary parts separately, we get,
$2\left| \left( x-2 \right)+iy \right|=\left| \left( x-1 \right)+iy \right|$
On solving the modulus on both the sides, we get,
$2\sqrt{{{\left( x-2 \right)}^{2}}+{{y}^{2}}}=\sqrt{{{\left( x-1 \right)}^{2}}+{{y}^{2}}}$
On taking the square root on both the sides of the above equation, we get,
$4\left[ {{\left( x-2 \right)}^{2}}+{{y}^{2}} \right]={{\left( x-1 \right)}^{2}}+{{y}^{2}}$
We know that ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$, so on applying this property in the above equation, we get,
$4\left[ {{x}^{2}}+4-4x+{{y}^{2}} \right]={{x}^{2}}+1-2x+{{y}^{2}}$
On solving it further, we get,
$4{{x}^{2}}+16-16x+4{{y}^{2}}={{x}^{2}}+1-2x+{{y}^{2}}$
On taking all the terms to one side, we get,
$\begin{align}
  & 4{{x}^{2}}-{{x}^{2}}-16x+2x+4{{y}^{2}}-{{y}^{2}}+16-1=0 \\
 & 3{{x}^{2}}+3{{y}^{2}}-14x+15=0 \\
\end{align}$
On dividing the whole equation by 3, we get,
${{x}^{2}}+{{y}^{2}}-\dfrac{14}{3}x+5=0$
By making perfect squares, we get,
$\begin{align}
  & {{\left( x-\dfrac{7}{3} \right)}^{2}}+{{y}^{2}}+5-\dfrac{49}{9}=0 \\
 & {{\left( x-\dfrac{7}{3} \right)}^{2}}+{{y}^{2}}-\dfrac{4}{9}=0 \\
 & {{\left( x-\dfrac{7}{3} \right)}^{2}}+{{y}^{2}}={{\left( \dfrac{2}{3} \right)}^{2}} \\
\end{align}$
Now, we know that the equation of a circle with the center $\left( \alpha ,\beta \right)$ and the radius r is \[{{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{r}^{2}}\].
So, on comparing both the equations, we get to know that,
${{\left( x-\dfrac{7}{3} \right)}^{2}}+{{y}^{2}}={{\left( \dfrac{2}{3} \right)}^{2}}$ is the equation of a circle with the center $\left( \dfrac{7}{3},0 \right)$ and the radius $\dfrac{2}{3}$.
So, the locus of z in equation $2\left| z-2 \right|=\left| z-1 \right|$ is also a circle.

Note: In equation (i), that is $\left| z-2-3i \right|=5$. We get,

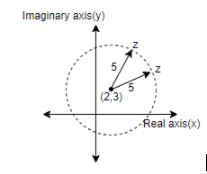
If we assume a complex number $\alpha =2+3i$, then $\left( z-\alpha \right)$ is also a complex number and $\left| z-\alpha \right|$ is the distance between z and $\alpha $, that is 5. So, whatever is z, the distance between z and a constant point, $\alpha $ is constant. So, this represents a circle.
So, $\left| z-\alpha \right|=r$ represents a circle with the center $\alpha $ and radius r.
In equation (ii), that is $2\left| z-2 \right|=\left| z-1 \right|$, we can also write it as $\dfrac{\left| z-2 \right|}{\left| z-1 \right|}=\dfrac{1}{2}$.
And, we know that in $\dfrac{\left| z-\alpha \right|}{\left| z-\beta \right|}=\dfrac{p}{q}$, locus of z is a circle with diameter endpoints, internal and external division of $\alpha $ and $\beta $ in the ratio p:q.
So, $\dfrac{\left| z-2 \right|}{\left| z-1 \right|}=\dfrac{1}{2}$ is a circle with the diametric end point A and B.

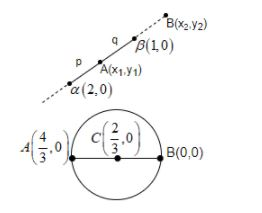
$\begin{align}
  & {{x}_{1}}=\dfrac{2+2}{3}=\dfrac{4}{3},{{y}_{1}}=\dfrac{0+0}{3}=0 \\
 & {{x}_{2}}=\dfrac{2-2}{3}=0,{{y}_{2}}=\dfrac{0-0}{3}=0 \\
\end{align}$