Question

If $\zeta $ is the set of boys in your school and $B$ is the set of boys who play badminton. Draw a Venn-diagram showing that some of the boys do not play badminton. If $n\left( \zeta \right)=40$ and $n\left( B' \right)=17$ , find how many people play badminton.

Answer 1

Hint: In this problem we need to draw the Venn diagram for the given condition and to find the number of boys who play badminton. We have given that $\zeta $ is the set of boys in your school and $B$ is the set of boys who play badminton and also we have the data $n\left( \zeta \right)=40$ and$n\left( B' \right)=17$. Here $n\left( \zeta \right)$ is the number of boys in the school and the set $B'$ is the reverse to the set $B$ that means $B'$ is the set of boys who do not play badminton. So the value $n\left( B' \right)$ is the number of boys who do not play badminton. Now we will find the number of boys who play badminton by subtracting the number of boys who do not play badminton from the total number of boys in the school and then we will draw the Venn diagram.

Complete step by step answer:
Given that, $\zeta $ is the set of boys in your school and $B$ is the set of boys who play badminton.
We also have the values $n\left( \zeta \right)=40$ and$n\left( B' \right)=17$.
Where $n\left( \zeta \right)$ is the total number of boys in the school.
$B'$ Is the reverse set of$B$. Hence the value $n\left( B' \right)$ is the number of boys who does not play badminton.
Now the number of boys who plays badminton in the school is represented by $n\left( B \right)$ and that is calculated by subtracting the number of boys who does not play badminton from the total number of boys in the school, then we will have
$\begin{align}
  & n\left( B \right)=n\left( \zeta \right)-n\left( B' \right) \\
 & \Rightarrow n\left( B \right)=40-17 \\
 & \therefore n\left( B \right)=23 \\
\end{align}$
Hence the total number of boys who play badminton is $23$ .
Now the Venn diagram comparing the total number of students in the school with number of students who play badminton is given below

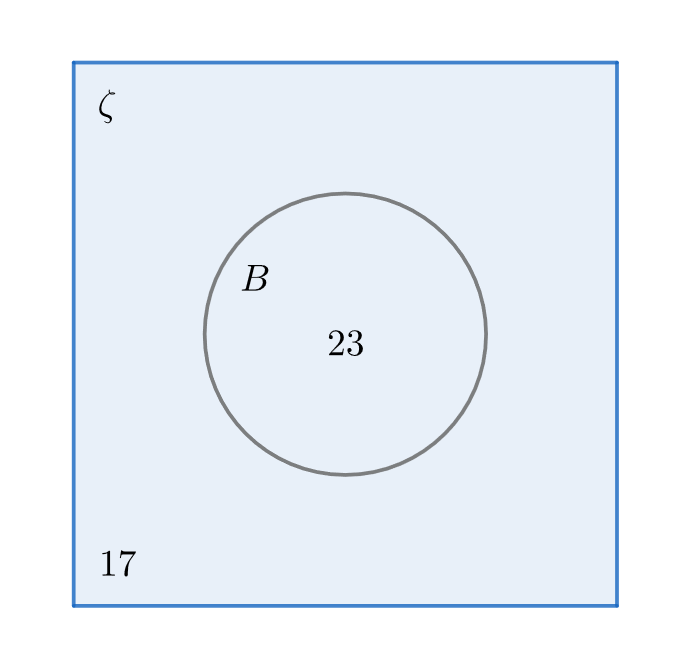
Note: In this problem we have asked to draw the Venn diagram which is the graphical representation of the relation between the two sets. In this problem we have the sets $\zeta $and$B$. Where $\zeta $ is the total number of boys in the school so we have taken it as a rectangle and $B$ is the set of boys who play badminton in the school. So we have drawn a circle inside the rectangle which shows that the set $B$ is the subset of$\zeta $.