Question

If ${{z}_{1}},{{z}_{2}},{{z}_{3}}$ and ${{z}_{4}}$ are complex numbers, show that they are vertices of a parallelogram, in this argand diagram of and only if ${{z}_{1}}+{{z}_{3}}={{z}_{2}}+{{z}_{4}}$.

Answer 1

Hint: For solving this question you should know about a parallelogram and the dimensions of a parallelogram and how the points intersect each other in it. So, the parallelogram is a four-sided plane rectilinear figure in which opposite sides are parallel to each other. A parallelogram consists of 4 vertices and also consists of 4 edges. And the parallelogram is of a quadrilateral type. It has no lines of symmetry.

Complete step-by-step solution:
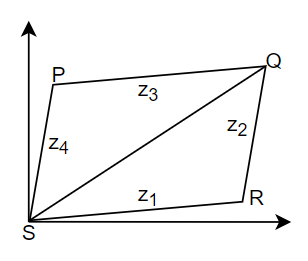
According to the question ${{z}_{1}},{{z}_{2}},{{z}_{3}}$ and ${{z}_{4}}$ are complex numbers and we have to show that they are vertices of a parallelogram, in this argand diagram of and only if ${{z}_{1}}+{{z}_{3}}={{z}_{2}}+{{z}_{4}}$. So, if we consider a parallelogram PQRS,

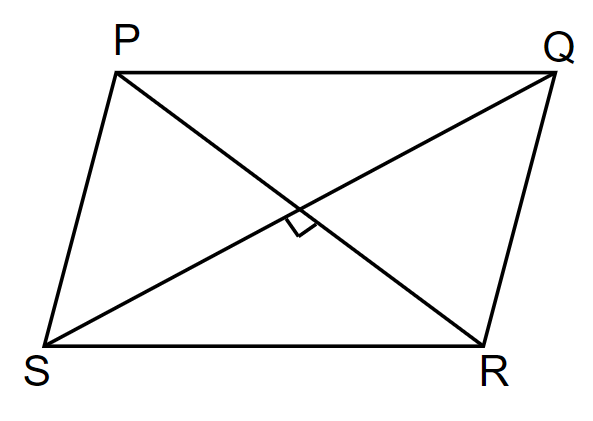
And if PQRS is a parallelogram, then PQ = RS and PS = RQ.
If we assume that ${{z}_{1}},{{z}_{2}},{{z}_{3}}$ and ${{z}_{4}}$ are the vertices of the parallelogram, therefore, midpoint of the diagonal coincide,
$\begin{align}
  & \Rightarrow \dfrac{{{z}_{1}}+{{z}_{3}}}{2}=\dfrac{{{z}_{2}}+{{z}_{4}}}{2} \\
 & \Rightarrow {{z}_{1}}+{{z}_{3}}={{z}_{2}}+{{z}_{4}} \\
\end{align}$
Now if we conversely assume that,
$\begin{align}
  & \Rightarrow {{z}_{1}}+{{z}_{3}}={{z}_{2}}+{{z}_{4}} \\
 & \Rightarrow \dfrac{{{z}_{1}}+{{z}_{3}}}{2}=\dfrac{{{z}_{2}}+{{z}_{4}}}{2} \\
\end{align}$
So, here we can say that the midpoint of the diagonals coincide.
Hence, ${{z}_{1}},{{z}_{2}},{{z}_{3}}$ and ${{z}_{4}}$ are the vertices of the parallelogram.

Note: When we solve this question, we have to make triangles which help us to solve the question in an easy way and they give us the correct answer possibilities too. These are also to help to calculate the complete area of a parallelogram. With the help of triangles we can easily calculate that.