Question

If z satisfies the inequality \[\left| z-1-2i \right|\le 1\], then
(a) \[\min \left( \arg (z) \right)={{\tan }^{-1}}\left( \dfrac{3}{4} \right)\]
(b) \[\max \left( \arg (z) \right)=\dfrac{\pi }{6}\]
(c) \[\min \left( \left| z \right| \right)=\sqrt{5}\]
(d) \[\max \left( \left| z \right| \right)=\sqrt{5}\]

Answer 1

Hint:First, before proceeding for this, we must draw the circle given by the inequality condition given in the question. Then, we have assumed in the figure the diameter of the circle joined to the origin makes an angle of $\theta $ with y-axis and tangent to the circle makes an angle of $\phi $ with the x-axis. Then, by checking all the options one by one, we get the correct option as an answer.

Complete step by step answer:
In this question, we are supposed to find the correct option from the given options when z satisfies the inequality \[\left| z-1-2i \right|\le 1\].
So, before proceeding for this, we must draw the circle given by the inequality condition given in the question as:

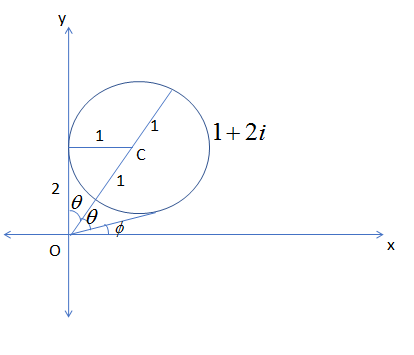
Now, we have assumed in the figure the diameter of the circle joined to the origin makes an angle of $\theta $ with y axis and tangent to the circle makes an angle of $\phi $ with x axis.
So, starting with the third option where r is the radius of the circle, we get:
min \[\left| z \right|\] = OC-r
Now, we can see from the figure that the radius of the circle is 1 and length of OC is given by Pythagoras theorem as:
$\begin{align}
  & O{{C}^{2}}={{2}^{2}}+{{1}^{2}} \\
 & \Rightarrow O{{C}^{2}}=4+1 \\
 & \Rightarrow O{{C}^{2}}=5 \\
 & \Rightarrow OC=\sqrt{5} \\
\end{align}$
So, we get the value of min(z) as:
$\min \left| z \right|=\sqrt{5}-1$
Now, we know from the conditions of inequality that if z minimum is $\sqrt{5}-1$, then the value of max z is given by:
$\max \left| z \right|=\sqrt{5}+1$
So, we can see that clearly options (c) and (d) are incorrect.
Now, we can clearly see from the figure that the value of maximum argument is:
\[\max \left( \arg (z) \right)=\dfrac{\pi }{2}\]
So, we get the option (b) as incorrect.
Now, to get the minimum argument by using the formula as:
$\phi =\dfrac{\pi }{2}-2\theta $
Then, by substituting the value of $\theta $given by the formula $\theta ={{\tan }^{-1}}\dfrac{1}{2}$ , we get:
$\begin{align}
  & \phi =\dfrac{\pi }{2}-2{{\tan }^{-1}}\dfrac{1}{2} \\
 & \Rightarrow \phi =\dfrac{\pi }{2}-{{\tan }^{-1}}\dfrac{1}{1-\dfrac{1}{4}} \\
 & \Rightarrow \phi =\dfrac{\pi }{2}-{{\tan }^{-1}}\dfrac{1}{\dfrac{3}{4}} \\
 & \Rightarrow \phi =\dfrac{\pi }{2}-{{\tan }^{-1}}\dfrac{4}{3} \\
 & \Rightarrow \phi ={{\tan }^{-1}}\dfrac{3}{4} \\
\end{align}$
So, we get the minimum argument as ${{\tan }^{-1}}\dfrac{3}{4}$.
Hence, option (a) is correct.
Note:
Now, to solve these type of the questions we need to know some of the basics by using the Pythagoras theorem for the right angles triangle which states that the square of the hypotenuse h is equal to the sum of the square of perpendicular p and base b as ${{h}^{2}}={{p}^{2}}+{{b}^{2}}$. Moreover, the formula used for trigonometry is given by $2{{\tan }^{-1}}x={{\tan }^{-1}}\left( \dfrac{2x}{1-{{x}^{2}}} \right)$.