Question

If $y=4x-5$ is a tangent to the curve ${{y}^{2}}=p{{x}^{3}}+q$ at (2, 3), then (p + q) is equal to:
A. – 5
B. 5
C. – 9
D. 9
E. 0

Answer 1

Hint: We start solving the problem by recalling the slope of tangent at a point on y = f (x) is given by the value of $\dfrac{dy}{dx}$ at that point. We first find $\dfrac{dy}{dx}$ and put x = 2 and y = 3 to get the slope of the tangent. We then equate the obtained value with the slope of the line y = 4x – 5 to get the value of p. We then substitute the point (2, 3) and the obtained value of p in the curve ${{y}^{2}}=p{{x}^{3}}+q$ to get the value of q. We then find \[\left( p+q \right)\] to get the desired result.

Complete step-by-step answer:
According to the question $y=4x-5$ is a tangent to the curve ${{y}^{2}}=p{{x}^{3}}+q$ at (2, 3).
Let us draw by showing all the given information.

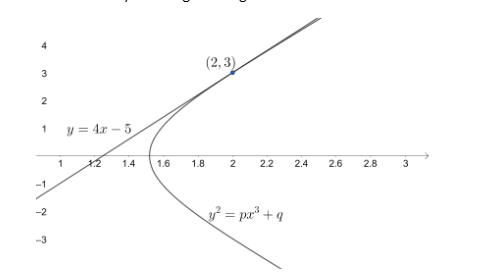
We know,
Slope of a tangent at any point (p, q) on the curve y = f (x) is given $\dfrac{d}{dx}f\left( x \right)$ at point (p, q).
Here, ${{y}^{2}}=p{{x}^{3}}+q$……………. (1)
Let us first find out the value of $\dfrac{dy}{dx}$.
Differentiating both sides with the respect of x, we will get,
$\Rightarrow 2y\dfrac{dy}{dx}=3p{{x}^{2}}$.
On dividing both sides of equation by 2y, we will get,
$\Rightarrow \dfrac{dy}{dx}=\dfrac{3p{{x}^{2}}}{2y}$.
To find value of $\dfrac{dy}{dx}$ at (2, 3), we will put x = 2 and y = 3 and we will get,
$\dfrac{dy}{dx}$= 2p
According to question tangent at this point is $''y=4x-5''$comparing this with slope from of equation of line i.e. y = mx + c, we will get,
‘m’ (slope) of this line = 4.
Equating this with the value of $\dfrac{dy}{dx}$ at (2, 3) obtained above, we will get,
$\Rightarrow 2p=4$.
$\Rightarrow p=2$.
Now, to find \[\left( p+q \right)\], we also need to find ‘q’.
According to question, point (2, 3) lie on ${{y}^{2}}=p{{x}^{3}}+q$, so the point (2, 3) will satisfy the equation ${{y}^{2}}=p{{x}^{3}}+q$.
$\Rightarrow {{\left( 3 \right)}^{2}}=p{{\left( 2 \right)}^{3}}+q$.
$\Rightarrow 9=p\left( 8 \right)+q$.
On putting “p = 2” as obtained above, we will get,
$\Rightarrow 9=\left( 2 \right)\left( 8 \right)+q$.
$\Rightarrow 9=16+q$.
Taking constant terms to RHS and ‘q’ to LHS, we will get,
$\Rightarrow -q=16-9$.
$\Rightarrow -q=7$.
Multiplying both sides of equation by “- 1”, we will get,
$\Rightarrow q=-7$.
So, the value of \[\left( p+q \right)\] will be \[2+\left( -\text{ }7 \right)=-5\].
Hence, \[p+q=-5\]
The correct option for the given problem is (A).

Note: We can also solve this problem by substituting the equation of tangent in the equation of the curve. If we do substitution, we get a cubic equation which is not an easy job to solve. We should not make errors while finding the derivative of the function and finding the slope. We need to know that the point lies on both tangent and the given curve. The tangent at the given point can intersect the curve at the other point as the given equation is not a standard one.