Question

If $y+b={{m}_{1}}(x+a)$ and $y+b={{m}_{2}}(x+a)$ ; $(a\ne b,{{m}_{1}}\ne {{m}_{2}})$ are two tangents to the parabola ${{y}^{2}}=4ax$, then ${{m}_{1}}{{m}_{2}}=-1$ .

Answer 1

Hint: Write the equation of pair of tangents using the formula for equation of pair of tangents ${{T}^{2}}=S{{S}_{1}}$ where $S={{y}^{2}}-4ax$ , ${{S}_{1}}={{y}_{1}}-4a{{x}_{1}}$ and $T=y{{y}_{1}}-2a(x+{{x}_{1}})$ when ${{y}^{2}}=4ax$ is the equation of parabola and $({{x}_{1}},{{y}_{1}})$is an external point. Here $(-a,-b)$ is the external point $({{x}_{1}},{{y}_{1}})$ . Also find equation of pair of tangents using the tangents $y+b={{m}_{1}}(x+a)$ and $y+b={{m}_{2}}(x+a)$. Compare both the equations to find the value of ${{m}_{1}}{{m}_{2}}$ .

Complete step by step answer:
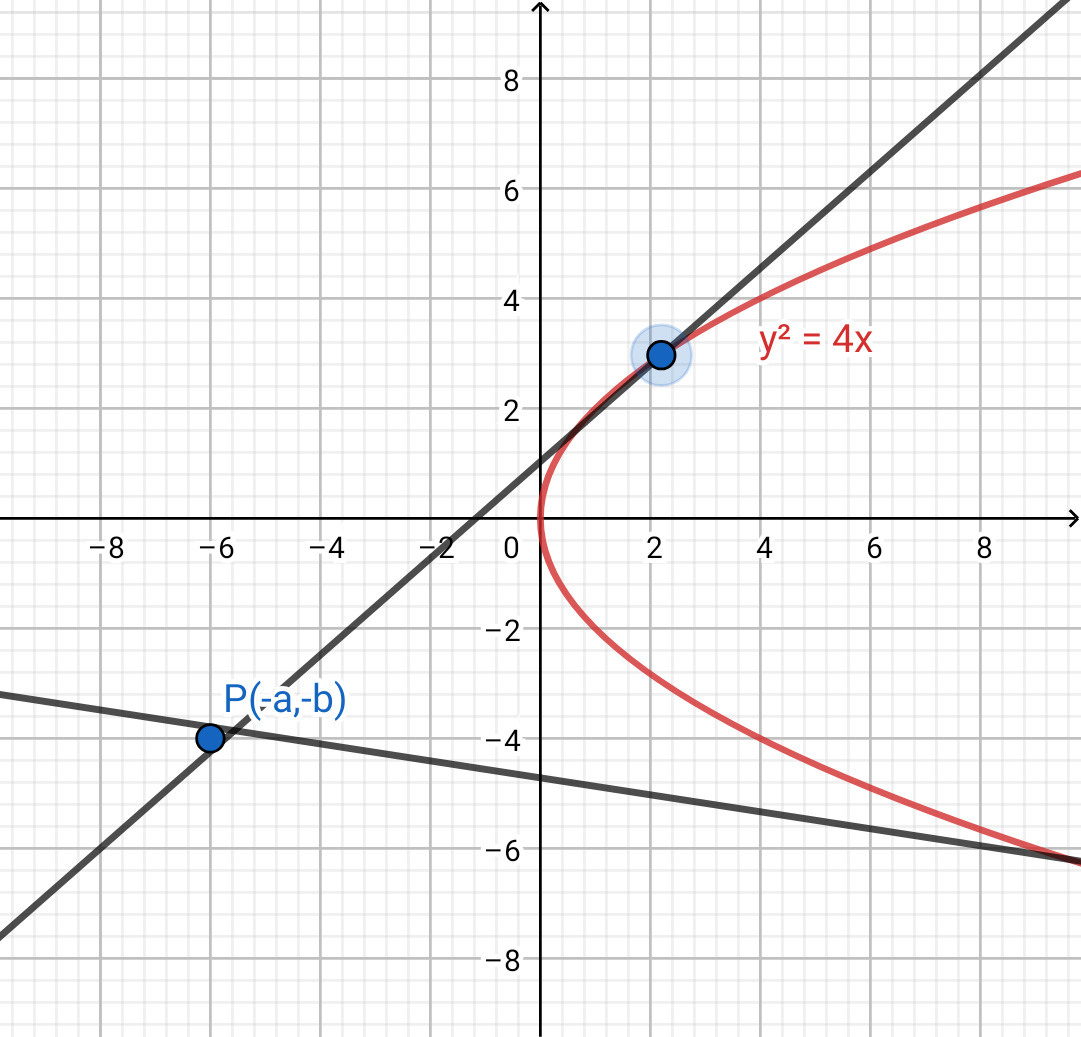
In the question we are given two equations of tangents $y+b={{m}_{1}}(x+a)$ and $y+b={{m}_{2}}(x+a)$ ; $(a\ne b,{{m}_{1}}\ne {{m}_{2}})$to the parabola ${{y}^{2}}=4ax$ . We can see that these two tangents are drawn at point $(-a,-b)$with slope ${{m}_{1}}$ and ${{m}_{2}}$ respectively because tangent is a line and equation of line when it passes from point $(p,q)$ with slope $m$ is given by $(y-q)=m(x-p)$ . So using this formula can say that two tangents are drawn at point $(-a,-b)$with slope ${{m}_{1}}$ and ${{m}_{2}}$ respectively.

Now we will find the equation of the pair of tangents. For this we will be using formula for equation of pair of tangents which is given by
 ${{T}^{2}}=S{{S}_{1}}........(1)$
 where $S={{y}^{2}}-4ax$ , ${{S}_{1}}={{y}_{1}}-4a{{x}_{1}}$ and $T=y{{y}_{1}}-2a(x+{{x}_{1}})$ when ${{y}^{2}}=4ax$ is the equation of parabola and $({{x}_{1}},{{y}_{1}})$is an external point. Here $(-a,-b)$ is the external point $({{x}_{1}},{{y}_{1}})$ . So we will find $T,S,{{S}_{1}}$ using this formula, so we get
$T=y(-b)-2a(x-a)$
$S={{y}^{2}}-4ax$
$\begin{align}
  & {{S}_{1}}={{(-b)}^{2}}-4a(-a) \\
 & ={{b}^{2}}+4{{a}^{2}} \\
\end{align}$
Now we will use equation (1) to find the equation of pair of tangents in which we will substitute the values of $T,S,{{S}_{1}}$ in equation (1), thus equation of pair of tangent becomes
${{(y(-b)-2a(x-a))}^{2}}=({{y}^{2}}-4ax)({{b}^{2}}+4{{a}^{2}})......(2)$
Now we will simplify the above equation, we will simplify the left hand side of the equation by squaring the terms and in the right hand side of the equation by multiplying the two terms.
$({{(-by)}^{2}}+{{(2a(x-a))}^{2}}-2(-by)2a(x-a))=({{y}^{2}}{{b}^{2}}+4{{a}^{2}}{{y}^{2}}-4ax{{b}^{2}}-16{{a}^{3}}x)$
${{b}^{2}}{{y}^{2}}+4{{a}^{2}}{{(x-a)}^{2}}+4aby(x-a)={{y}^{2}}{{b}^{2}}+4{{a}^{2}}{{y}^{2}}-4ax{{b}^{2}}-16{{a}^{3}}x$
Further simplify the term ${{(x-a)}^{2}}$ by using the formula ${{(p-q)}^{2}}={{p}^{2}}+{{q}^{2}}-2pq$.
${{b}^{2}}{{y}^{2}}+4{{a}^{2}}({{x}^{2}}-2ax+{{a}^{2}})+4aby(x-a)={{y}^{2}}{{b}^{2}}+4{{a}^{2}}{{y}^{2}}-4ax{{b}^{2}}-16{{a}^{3}}x$
${{b}^{2}}{{y}^{2}}+4{{a}^{2}}{{x}^{2}}-8{{a}^{3}}x+4{{a}^{4}}+4abxy-4{{a}^{2}}by={{y}^{2}}{{b}^{2}}+4{{a}^{2}}{{y}^{2}}-4ax{{b}^{2}}-16{{a}^{3}}x$
Now we will shift all the terms on the left hand side to the right hand side and combine the like terms. So the equation now becomes.
 $({{b}^{2}}{{y}^{2}}-{{y}^{2}}{{b}^{2}})+4{{a}^{2}}{{x}^{2}}+(16{{a}^{3}}x-8{{a}^{3}}x)+4{{a}^{4}}+4abxy-4{{a}^{2}}by-4{{a}^{2}}{{y}^{2}}+4ax{{b}^{2}}=0$
$4{{a}^{2}}{{x}^{2}}+8{{a}^{3}}x+4{{a}^{4}}+4abxy-4{{a}^{2}}by-4{{a}^{2}}{{y}^{2}}+4ax{{b}^{2}}=0$
We will further simplify by dividing the above equation by $4a$ throughout.
$a{{x}^{2}}+2{{a}^{2}}x+{{a}^{3}}+bxy-aby-a{{y}^{2}}+x{{b}^{2}}=0..........(3)$
Also from the question the two equation of tangents are $y+b={{m}_{1}}(x+a)$ and $y+b={{m}_{2}}(x+a)$
If these two tangents form a pair of tangents then equation of pair of tangents in given by
 $[(y+b)-{{m}_{1}}(x+a)][(y+b)-{{m}_{2}}(x+a)]=0$
Simplify the above equation by multiplying the two terms in the bracket. After multiplying we get,
${{(y+b)}^{2}}-{{m}_{2}}(y+b)(x+a)-{{m}_{1}}(x+a)(y+b)+{{m}_{1}}{{m}_{2}}{{(x+a)}^{2}}=0$
The above equation on further simplification we get,
$({{y}^{2}}+{{b}^{2}}+2by)-({{m}_{1}}+{{m}_{2}})(y+b)(x+a)+{{m}_{1}}{{m}_{2}}({{x}^{2}}+{{a}^{2}}+2xa)=0$
 ${{y}^{2}}+{{b}^{2}}+2by+{{m}_{1}}{{m}_{2}}{{x}^{2}}+{{m}_{1}}{{m}_{2}}{{a}^{2}}+{{m}_{1}}{{m}_{2}}2xa-({{m}_{1}}+{{m}_{2}})(y+b)(x+a)=0......(4)$
Since equation (3) and (4) both represent equation of pair of tangents then coefficients of $x,y,{{x}^{2}},{{y}^{2}}$ are equal in both the equations. Now we will compare both the equation (3) and (4) to find the value of ${{m}_{1}}{{m}_{2}}$ . Comparing the coefficients of ${{x}^{2}}$in both equations we get
 ${{m}_{1}}{{m}_{2}}=a........(5)$
Now we will find out the value of $a$ by comparing the coefficient of ${{y}^{2}}$ we get $-a=1$ that implies $a=-1$. So substituting the value of $a$ in equation (5) we get
 ${{m}_{1}}{{m}_{2}}=-1$
Hence, if $y+b={{m}_{1}}(x+a)$ and $y+b={{m}_{2}}(x+a)$ ; $(a\ne b,{{m}_{1}}\ne {{m}_{2}})$ are two tangents to the parabola ${{y}^{2}}=4ax$, then ${{m}_{1}}{{m}_{2}}=-1$ .

Note:
For equation of pair of tangents of parabola, formula is given by ${{T}^{2}}=S{{S}_{1}}$ where $S={{y}^{2}}-4ax$ , ${{S}_{1}}={{y}_{1}}-4a{{x}_{1}}$ and $T=y{{y}_{1}}-2a(x+{{x}_{1}})$ when ${{y}^{2}}=4ax$ is the equation of parabola and $({{x}_{1}},{{y}_{1}})$is an external point. Care should be taken while comparing the coefficients of equation ${{y}^{2}}+{{b}^{2}}+2by+{{m}_{1}}{{m}_{2}}{{x}^{2}}+{{m}_{1}}{{m}_{2}}{{a}^{2}}+{{m}_{1}}{{m}_{2}}2xa-({{m}_{1}}+{{m}_{2}})(y+b)(x+a)=0$ and $a{{x}^{2}}+2{{a}^{2}}x+{{a}^{3}}+bxy-aby-a{{y}^{2}}+x{{b}^{2}}=0$ to find the value of ${{m}_{1}}{{m}_{2}}$ . Proper attention must be paid while comparing.