Question

If x−y=7 and xy =9, then find the value of algebraic equation (\[{{\text{x}}^2} + {{\text{y}}^2}\]).

Answer 1

HINT- To proceed the solution of this question, by visualising any known identity after squaring where we can put the values of known expression and get the desired expression.

Complete step-by-step answer:
In the question it is given two equation x−y=7 and xy =9
Let x−y=7 …………. (1)
And xy =9…………. (2)

Squaring equation (1) from both side
⇒${\left( {{\text{x - y}}} \right)^2} = {7^2}$

We know that,
⇒${\left( {{\text{a - b}}} \right)^2} = \left( {{{\text{a}}^2} + {{\text{b}}^2} - 2{\text{ab}}} \right)$

Here, variable a = x and b=y, so their square using ${\left( {{\text{a - b}}} \right)^2} = \left( {{{\text{a}}^2} + {{\text{b}}^2} - 2{\text{ab}}} \right)$
⇒${{\text{x}}^2} + {{\text{y}}^2} - 2{\text{xy}} = 49$ ………. (3)

In the question it is given xy =9

Hence on putting xy =9
⇒${{\text{x}}^2} + {{\text{y}}^2} - 2 \times 9 = 49$
On further solving
⇒${{\text{x}}^2} + {{\text{y}}^2} = 49 + 18$
⇒${{\text{x}}^2} + {{\text{y}}^2} = 67$

Hence the value of algebraic equation (\[{{\text{x}}^2} + {{\text{y}}^2}\]) = 67

Note-
In this particular question. Graphically we can also calculate values of x and y

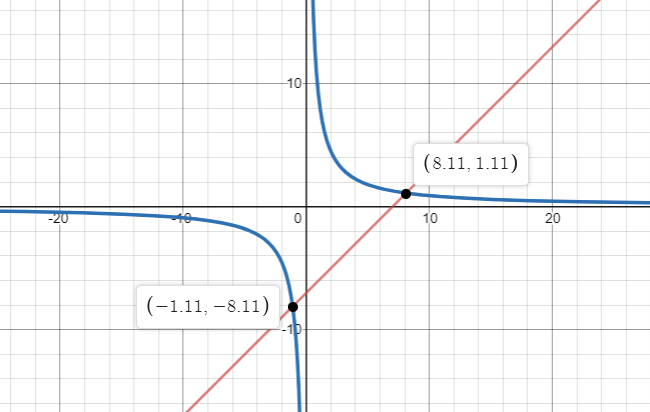
Here, we got two intersection points, (8.11,1.11) and (-1.11.-8.11) which will be the corresponding values of x and y at different points.
So value of \[{{\text{x}}^2} + {{\text{y}}^2}{\text{ = 8}}{\text{.1}}{{\text{1}}^2} + {1.11^2} \approx 67\] at Point (8.11,1.11)
⇒\[{{\text{x}}^2} + {{\text{y}}^2}{\text{ = }}{\left( { - 1.11} \right)^2} + {\left( {{\text{ - 8}}{\text{.11}}} \right)^2} \approx 67\] at point (-1.11.-8.11)