Question

If \[x\sin {45^ \circ }{\cos ^2}{60^ \circ } = \dfrac{{{{\tan }^2}{{60}^ \circ }\cos ec{{30}^ \circ }}}{{\sec {{45}^ \circ }{{\cot }^2}{{30}^ \circ }}}\] then \[x = \]
A.\[2\]
B.\[4\]
C.\[8\]
D.\[16\]

Answer 1

Hint: Trigonometric functions are also known as Circular Functions can be simply defined as the functions of an angle of a triangle. It means that the relationship between the angles and sides of a triangle are given by these trig functions. The basic trigonometric functions are sine, cosine, tangent, cotangent, secant and cosecant.

Complete step-by-step answer:
The angles of sine, cosine, and tangent are the primary classification of functions of trigonometry. And the three functions which are cotangent, secant and cosecant can be derived from the primary functions. Basically, the other three functions are often used as compared to the primary trigonometric functions.

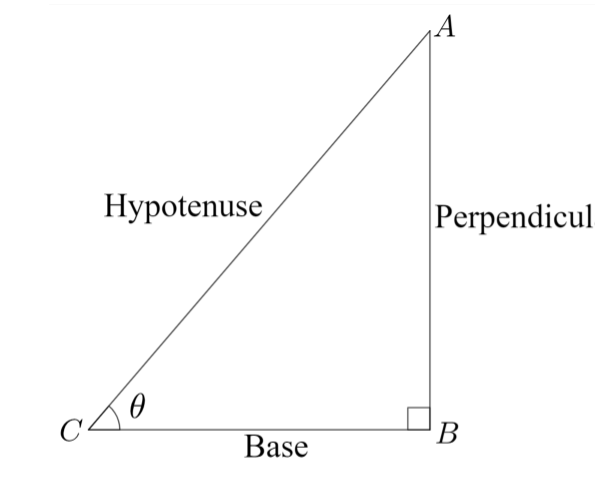
Sine: \[\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}\]
Cosine: \[\cos \theta = \dfrac{{base}}{{hypotenuse}}\]
Tangent: \[\cos \theta = \dfrac{{perpendicular}}{{base}}\]
The Secant, the cosecant (csc) and the cotangent are the three additional functions which are derived from the primary functions of sine, cos, and tan. The reciprocal of the sine, the cos, and the tan are the cosecant (csc), the secant (sec), and the cotangent (cot) respectively.
Inverse trigonometric functions are used to obtain an angle from any of the angle’s trigonometric ratios. Basically, inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions are represented as arcsin, arccosine, arctangent, arc cotangent, arc secant, and arc cosecant.
We are given \[x\sin {45^ \circ }{\cos ^2}{60^ \circ } = \dfrac{{{{\tan }^2}{{60}^ \circ }\cos ec{{30}^ \circ }}}{{\sec {{45}^ \circ }{{\cot }^2}{{30}^ \circ }}}\]
Putting the values if respective trigonometric functions we get ,
\[x\left( {\dfrac{1}{{\sqrt 2 }}} \right){\left( {\dfrac{1}{2}} \right)^2} = \dfrac{{{{\left( {\sqrt 3 } \right)}^2}(2)}}{{\left( {\sqrt 2 } \right){{\left( {\sqrt 3 } \right)}^2}}}\]
Which simplifies to
\[\dfrac{x}{{4\sqrt 2 }} = \sqrt 2 \]
Therefore we get
\[x = 8\]
Therefore option (3) is the correct answer.
So, the correct answer is “Option 3”.

Note: The angles of sine, cosine, and tangent are the primary classification of functions of trigonometry. And the three functions which are cotangent, secant and cosecant can be derived from the primary functions.