Question

If \[{{x}^{2}}+{{y}^{2}}-2x+2ay+a+3=0\] represents a real circle with non – zero radius, then most appropriate is?
A. $a\in \left( -\infty ,-1 \right)$
B. $a\in \left( -1,2 \right)$
C. $a\in \left( 2,\infty \right)$
D. $a\in \left( -\infty ,-1 \right)\cup \left( 2,\infty \right)$

Answer 1

Hint: We will start by using the fact that a circle with radius r and centre at $\left( h,k \right)$ is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$. Then we will convert the given equation in the similar form and use the fact that the quantity inside a square root can’t be negative to find the range of a.
Complete step-by-step answer:
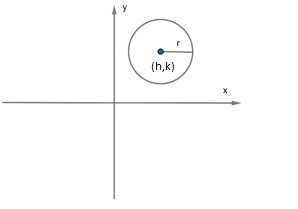
Now, we have the equation of a circle as ${{x}^{2}}+{{y}^{2}}-2x+2ay+a+3=0$ and the circle had non – zero radius. Now, we know that the general equation of a circle with centre at $\left( h,k \right)$ and radius r is ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$.

Now, we have the equation of a circle as ${{x}^{2}}-2x+{{y}^{2}}+2ay+a+3=0$.
Now, we will complete the square with respect to x and y by adding and subtracting the $\dfrac{1}{2}$ of the coefficient of x and y. So, we have,
${{x}^{2}}-2x+{{\left( 1 \right)}^{2}}-{{\left( 1 \right)}^{2}}+{{y}^{2}}+2ay+{{a}^{2}}-{{a}^{2}}+a+3=0$
Now, we know that,
$\begin{align}
  & {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab \\
 & {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab \\
\end{align}$
So, applying this to the above equation, we have,
$\begin{align}
  & {{\left( x-1 \right)}^{2}}-1+{{\left( y+a \right)}^{2}}-{{a}^{2}}+a+3=0 \\
 & {{\left( x-1 \right)}^{2}}+{{\left( y+a \right)}^{2}}+a-{{a}^{2}}+2=0 \\
 & {{\left( x-1 \right)}^{2}}+{{\left( y+a \right)}^{2}}={{a}^{2}}-a-2 \\
 & {{\left( x-1 \right)}^{2}}+{{\left( y-\left( -a \right) \right)}^{2}}={{a}^{2}}-a-2 \\
\end{align}$
Now, on comparing with ${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$ we have the radius of circle as $r=\sqrt{{{a}^{2}}-a-2}$.
Now, we know that the quantity inside a square root is always non – negative. So, we have,
\[\begin{align}
  & {{a}^{2}}-a-2\ge 0 \\
 & {{a}^{2}}-2a+a-2\ge 0 \\
 & a\left( a-2 \right)+1\left( a-2 \right)\ge 0 \\
 & \left( a+1 \right)\left( a-2 \right)\ge 0 \\
\end{align}\]
Now, we have the point at which ${{a}^{2}}-a-2=0$ as $a=2,a=-1$. Now, we represent this range on a number line and the sign depicting the nature of ${{a}^{2}}-a-2$.

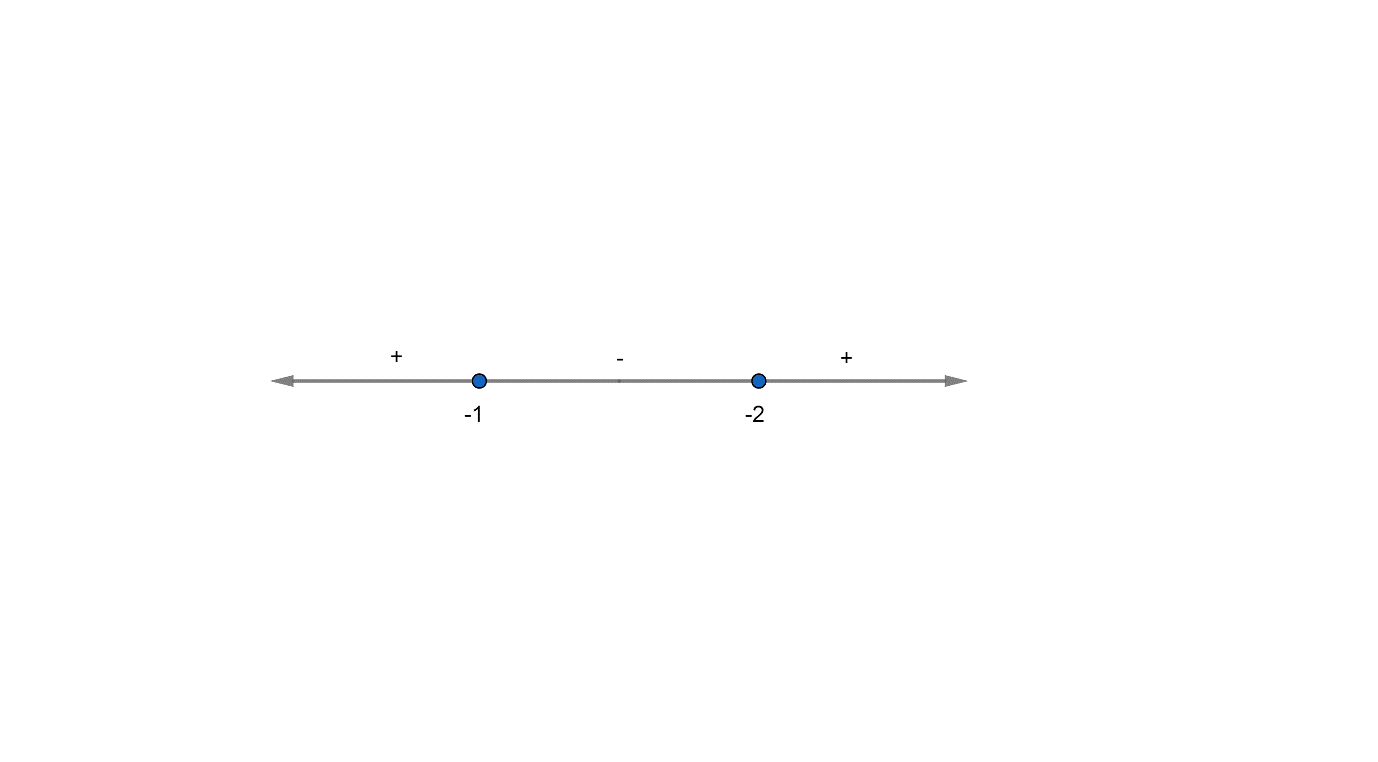
So, we have,
$\left( a+1 \right)\left( a-2 \right)\ge 0$ for $a\in \left( -\infty ,-1 \right)\cup \left( 2,\infty \right)$
Hence, the correct option is (D).

Note: It is important to note that we have used fact given in the question that the circle is real and has non – zero radius. Also, it is important to note that we have not taken the value of $a=-1\ and\ a=2$ because the value radius of the circle is zero which contradicts the fact that the circle is real with non – zero radius.