Question

If ${{x}^{2}}+6x-27>0$ and $-{{x}^{2}}+3x+4>0$, then $x$ lies in interval –

(a) $\left( 3,4 \right)$
(b) $\left[ 3,4 \right]$
(c) $\left( -\infty ,3 \right)\cup \left( 4,\infty \right)$
(d) $\left( -9,4 \right)$

Answer 1

Hint:This question involves inequality. We have to find the value of $x$ that satisfies both the inequalities. By following the concept of inequality, we will solve for an interval of $x$.

Complete step by step answer:
Concept: Let a polynomial $p\left( x \right)$is given –
$p\left( x \right)=\left( x-\alpha \right)\left( x-\beta \right)$
Firstly we find the critical points by solving for $p\left( x \right)=0$.
$\left( x-\alpha \right)\left( x-\beta \right)=0$
$\Rightarrow x=\alpha $and $\Rightarrow x=\beta $.

Let $\beta >\alpha $. So,

For $x>\beta $. As $\left( x-\beta \right)$ and $\left( x-\alpha \right)$ will be positive, so \[p\left( x \right)=\left( x-\alpha \right)\left( x-\beta \right)\] will be positive.

For $\alpha < x<\beta $. As $\left( x-\beta \right)$ will be negative and $\left( x-\alpha \right)$ will be positive, so $p\left( x \right)=\left( x-\alpha \right)\left( x-\beta \right)$ will be negative.

For $x<\alpha $, As $\left( x-\beta \right)$ and $\left( x-\alpha \right)$ both will be negative, then \[p\left( x \right)=\left( x-\alpha \right)\left( x-\beta \right)\] will be positive.
So for, \[p\left( x \right)=\left( x-\alpha \right)\left( x-\beta \right)>0\]
$\Rightarrow x\in \left( -\infty ,\alpha \right)\cup \left( \beta ,\infty \right)$
And for, \[p\left( x \right)=\left( x-\alpha \right)\left( x-\beta \right)<0\]
$\Rightarrow x\in \left( \alpha ,\beta \right)$

Now for inequality (i),
${{x}^{2}}+6x-27>0$
$\Rightarrow {{x}^{2}}+9x-3x-27>0$
$\Rightarrow x\left( x+9 \right)-3\left( x+9 \right)>0$
$\Rightarrow \left( x-3 \right)\left( x+9 \right)>0$

Let us assume $p\left( x \right)=\left( x-3 \right)\left( x+9 \right)$ for critical points.
$p\left( x \right)=0$
$\Rightarrow \left( x-3 \right)\left( x+9 \right)=0$
$x=3$ and $x=-9$



For $x>3$,
\[p\left( x \right)=\left( x-3 \right)\left( x+9 \right)>0\]

For $-9< x<3$,
\[p\left( x \right)=\left( x-3 \right)\left( x+9 \right)<0\]

For $x<-9$,
\[p\left( x \right)=\left( x-3 \right)\left( x+9 \right)>0\]

So for \[\left( x-3 \right)\left( x+9 \right)>0\],
$\Rightarrow x\in \left( -\infty ,-9 \right)\cup \left( 3,\infty \right)$

Now for inequality (ii),
$-{{x}^{2}}+3x+4>0$
$\Rightarrow -\left( {{x}^{2}}-3x-4 \right)>0$
By multiplying $\left( -1 \right)$on both sides, inequality sign will change.
$\Rightarrow \left( {{x}^{2}}-3x-4 \right)<0$
$\Rightarrow x\left( x-4 \right)+\left( x-4 \right)<0$
$\Rightarrow \left( x-4 \right)\left( x+1 \right)<0$

Let us assume $q\left( x \right)=\left( x+1 \right)\left( x-4 \right)$. So for critical points, $q\left( x \right)=0$
$\left( x+1 \right)\left( x-4 \right)=0$
$\Rightarrow x=-1$ and $x=4$

For $x>4$,
$q\left( x \right)=\left( x+1 \right)\left( x-4 \right)>0$

For $-1< x<4$,
$q\left( x \right)=\left( x+1 \right)\left( x-4 \right)<0$

For $x<-1$,
$q\left( x \right)=\left( x+1 \right)\left( x-4 \right)<0$

So for, $q\left( x \right)=\left( x+1 \right)\left( x-4 \right)<0$
$\Rightarrow x\in \left( -1,4 \right)$

Now for an interval of $x$, we have to take the intersection of $x's$ interval for inequality (i) and inequality(ii).
For inequality (i),

For inequality (ii),

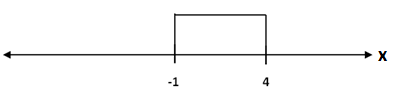
So, the intersection of both intervals –

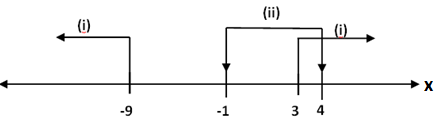
Hence, $x\in \left( 3,4 \right)$, and the correct option is (a).

Note:
 In this question, we have to solve inequality. So we have to take care of the inequality sign. If we multiply negative value on both sides of the inequality sign, then the inequality sign will definitely change. So students should keep in mind this property.