Question

If \[{{x}^{2}}+2hxy+{{y}^{2}}=0(h\ne 0)\] represents the equations of the straight lines through the origin (having slopes \[{{m}_{1}}\]and \[{{m}_{2}}\]) which make an angle \[\alpha \] with the straight line\[y+x=0\] then
(a). \[\text{sec 2}\alpha =h\]
(b). \[\cos \alpha =\sqrt{\dfrac{1+h}{2h}}\]
(c). \[{{m}_{1}}+{{m}_{2}}=-2\sec 2\alpha \]
(d). \[\cot \alpha =\sqrt{\dfrac{h+1}{h-1}}\]

Answer 1

- Hint: The given equation of the straight line represents two lines. Find out the slope of the pair of straight lines. The formula of angle between two lines having slopes \[{{m}_{1}},{{m}_{2}}\] is given by the formula, \[\tan \alpha =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\] . Apply this formula to obtain the angle between the pair of lines. Now convert the obtained angle into the desired result.



Complete step-by-step solution -

 The equations of straight line through origin is \[{{x}^{2}}+2hxy+{{y}^{2}}=0(h\ne 0)\].
As it is given that the slope of the lines are \[{{m}_{1}}\]and \[{{m}_{2}}\], so the equations of the pair of lines be \[y={{m}_{1}}x\] and \[y={{m}_{2}}x\].
It is also given that the pair of lines is making an angle \[\alpha \] with the straight line\[y+x=0\] as shown below,

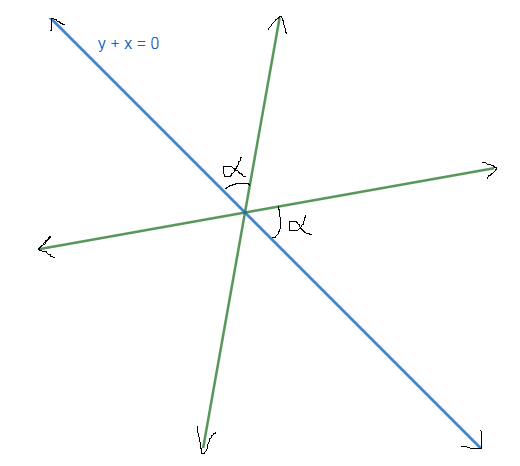
\[y+x=0\] can be written as \[y=-x\], comparing this with the general equation of line, i.e., \[y=mx+c\], the slope of this line is \['-1'\].
We know angle between two lines having slopes \[{{m}_{1}},{{m}_{2}}\] is given by the formula,
\[\tan \alpha =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\]
Now we will find the angle between line \[y={{m}_{1}}x\]and \[y+x=0\], we have
\[\begin{align}
  & \tan \alpha =\dfrac{{{m}_{1}}-(-1)}{1+{{m}_{1}}(-1)} \\
 & \Rightarrow \tan \alpha =\dfrac{{{m}_{1}}+1}{1-{{m}_{1}}} \\
 & \Rightarrow \tan \alpha (1-{{m}_{1}})=1+{{m}_{1}} \\
 & \Rightarrow \tan \alpha -{{m}_{1}}\tan \alpha =1+{{m}_{1}} \\
\end{align}\]
Bringing like terms on one side, we get
\[\begin{align}
  & \tan \alpha -1={{m}_{1}}+{{m}_{1}}\tan \alpha \\
 & \Rightarrow {{m}_{1}}(1+\tan \alpha )=\tan \alpha -1 \\
 & \Rightarrow {{m}_{1}}=\dfrac{\tan \alpha -1}{\tan \alpha +1}.........(i) \\
\end{align}\]
Now we will find the angle between line \[y+x=0\] and \[y={{m}_{2}}x\], we have
\[\begin{align}
  & \tan \alpha =\dfrac{(-1)-{{m}_{2}}}{1+{{m}_{2}}(-1)} \\
 & \Rightarrow \tan \alpha =\dfrac{-({{m}_{2}}+1)}{1-{{m}_{2}}} \\
 & \Rightarrow \tan \alpha (1-{{m}_{2}})=-(1+{{m}_{2}}) \\
 & \Rightarrow \tan \alpha -{{m}_{2}}\tan \alpha =-(1+{{m}_{2}}) \\
\end{align}\]
Bringing like terms on one side, we get
\[\begin{align}
  & \tan \alpha +1={{m}_{2}}\tan \alpha -{{m}_{2}} \\
 & \Rightarrow {{m}_{2}}(\tan \alpha -1)=\tan \alpha +1 \\
 & \Rightarrow {{m}_{2}}=\dfrac{\tan \alpha +1}{\tan \alpha -1}.........(ii) \\
\end{align}\]
Now as per the theorem, if \[a{{x}^{2}}+2hxy+b{{y}^{2}}=0\] is the equation of the lines with slope \[{{m}_{1}},{{m}_{2}}\], then sum of slopes is given by the formula,
\[{{m}_{1}}+{{m}_{2}}=\dfrac{-2h}{b}\]
Using this formula and substituting our values from equation (i) and (ii), we get
\[\left( \dfrac{\tan \alpha -1}{\tan \alpha +1} \right)+\left( \dfrac{\tan \alpha +1}{\tan \alpha -1} \right)=\dfrac{-2h}{b}\]
And from the given equation of line \[{{x}^{2}}+2hxy+{{y}^{2}}=0(h\ne 0)\], we see that \['b=1'\] , so above equation becomes,
\[\begin{align}
  & \left( \dfrac{\tan \alpha -1}{\tan \alpha +1} \right)+\left( \dfrac{\tan \alpha +1}{\tan \alpha -1} \right)=-2 \\
 & \Rightarrow \dfrac{{{(\tan \alpha -1)}^{2}}+{{(\tan \alpha +1)}^{2}}}{(\tan \alpha +1)(\tan \alpha -1)}=-2h \\
 & \Rightarrow \dfrac{{{(\tan \alpha -1)}^{2}}+{{(\tan \alpha +1)}^{2}}}{({{\tan }^{2}}\alpha -1)}=-2h \\
\end{align}\]
Now opening the brackets, we get
\[\begin{align}
  & \Rightarrow \dfrac{{{\tan }^{2}}\alpha +1-2\tan \alpha +{{\tan }^{2}}\alpha +1+2\tan \alpha }{({{\tan }^{2}}\alpha -1)}=-2h \\
 & \Rightarrow \dfrac{2({{\tan }^{2}}\alpha +1)}{({{\tan }^{2}}\alpha -1)}=-2h \\
 & \Rightarrow -\dfrac{({{\tan }^{2}}\alpha +1)}{({{\tan }^{2}}\alpha -1)}=h \\
\end{align}\]
But we know, \[\tan \alpha =\dfrac{\sin \alpha }{\cos \alpha }\], so above equation becomes,
\[\begin{align}
  & \Rightarrow -\dfrac{\left( \dfrac{{{\sin }^{2}}\alpha }{{{\cos }^{2}}\alpha }+1 \right)}{\left( \dfrac{{{\sin }^{2}}\alpha }{{{\cos }^{2}}\alpha }-1 \right)}=h \\
 & \Rightarrow -\dfrac{\left( \dfrac{{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha }{{{\cos }^{2}}\alpha } \right)}{\left( \dfrac{{{\sin }^{2}}\alpha -{{\cos }^{2}}\alpha }{{{\cos }^{2}}\alpha } \right)}=h \\
 & \Rightarrow -\dfrac{{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha }{{{\sin }^{2}}\alpha -{{\cos }^{2}}\alpha }=h \\
\end{align}\]
We know, \[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\] , so above equation becomes,
\[\begin{align}
  & \Rightarrow -\dfrac{1}{{{\sin }^{2}}\alpha -{{\cos }^{2}}\alpha }=h \\
 & \Rightarrow \dfrac{1}{{{\cos }^{2}}\alpha -{{\sin }^{2}}\alpha }=h \\
\end{align}\]
But we know, \[{{\cos }^{2}}\alpha -{{\sin }^{2}}\alpha =\cos 2\alpha \], we get
\[\Rightarrow h=\dfrac{1}{\cos 2\alpha }\]
But, \[\dfrac{1}{\cos \alpha }=\sec \alpha \], so above equation becomes,
\[\Rightarrow h=\sec 2\alpha \]
Hence the correct answer is option (a).

Note: The possibility of mistake is that the student can come to the conclusion that ${{m}_{1}}$ and ${{m}_{2}}$ are equal by applying the angle between the two lines formula. But this will lead to the wrong answer as if the slopes are equal then there won’t be two lines. So take care of this.