Question

If x is greater than 2, then $\left| {2 - \left. x \right|} \right.$ is equal to

Answer 1

Hint: The function described in this question is modulus function. Modulus function is always positive.
Modulus function is given by:
$\left| {\left. x \right|} \right. = x$, if x > 0
=$ - x$ , if x < 0
= 0 , if x=0
Here we have to first find the value in the modulus positive or negative. If value in the modulus is positive then modulus value of it remains the same and If value in the modulus is negative then modulus value is negative of actual value in modulus.

Complete step-by-step solution:
Here the question is to find the value of $\left| {2 - \left. x \right|} \right.$ .
Given that x is greater than 2 $ \Rightarrow x > 2$
$\begin{align}
&x > 2 \\
&\Rightarrow x - 2 > 0 \\
&\Rightarrow - (2 - x) > 0 \\
&\Rightarrow (2 - x) < 0 \\
\end{align} $
Here we achieved that $(2 - x) < 0$ that implies the term in the modulus in the question is negative .So by the definition of modulus function
$\left| {2 - \left. x \right|} \right. = - (2 - x)$ if $(2 - x) < 0$
So
$\begin{align}
&\left| {2 - \left. x \right|} \right. = - (2 - x) \\
&\Rightarrow \left| {2 - \left. x \right|} \right. = - 2 + x \\
&\Rightarrow \left| {2 - \left. x \right|} \right. = x - 2 \\
\end{align} $
The graph of $\left| {2 - \left. x \right|} \right.$ is given below

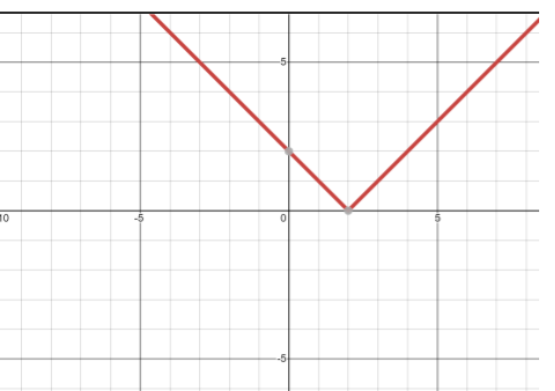
It is graph of whole $\left| {2 - \left. x \right|} \right.$ and the graph of $\left| {2 - \left. x \right|} \right.$ for $x > 2$ is taken from
(2, 0) where curve is intersecting X – axis .The $\left| {2 - \left. x \right|} \right.$ curve intersects Y-axis at (0, 2)

Note: The modulus functions are always positive and lies always above the X – axis. The modulus functions have a V – shaped graph containing a mirror line.
If x < 2 then $\left| {2 - \left. x \right|} \right.$ =$2 - x$ , Left side of curve from (2, 0) represents this portion.
If x = 2 then $\left| {2 - \left. x \right|} \right.$=0, The point (2, 0) represents this part.
Modulus function of complex number \[z{\text{ }} = x + iy\] (i = \[\sqrt { - 1} \]) is ${x^2} + {y^2}$ which is called modulus or absolute value of z.