Question

If \[x = {20^ \circ }\] and \[y = {30^ \circ }\] in the figure given below, what is the value of Z?

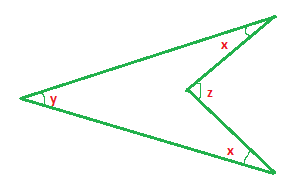
Answer 1

Hint: In this geometrical problem we will use the property that an exterior angle of a triangle is equal to the sum of its opposite interior angles. We need to consider the triangles from the figure and name them. Details are given in solution.

Complete step-by-step answer:

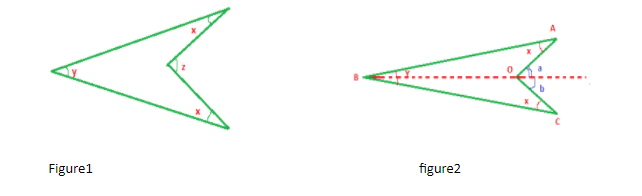
Now we can clearly see the construction we have done for the purpose to get the solution.
We can see two triangles in the figure2. ∆ABO and ∆CBO.
Now in ∆ABO:
 \[\angle a\] is the exterior angle of this triangle.
So using the property that an exterior angle of a triangle is equal to the sum of its opposite interior angles.
\[
   \Rightarrow \angle a = \angle ABO + \angle BAO \\
   \Rightarrow \angle a = \angle ABO + \angle x \\
\]
Now in ∆CBO:
 \[\angle b\] is the exterior angle of this triangle.
Again using the same property,
\[
   \Rightarrow \angle b = \angle CBO + \angle BCO \\
   \Rightarrow \angle b = \angle CBO + \angle x \\
\]
And from figure2 we can see that
\[\angle z = \angle a + \angle b\]
So putting the values from equations above
\[
   \Rightarrow \angle z = \angle ABO + \angle x + \angle CBO + \angle x \\
   \Rightarrow \angle z = \angle ABO + \angle CBO + 2\angle x \\
\]
But \[\angle ABO + \angle CBO = \angle y\]
Then
\[ \Rightarrow \angle z = \angle y + 2\angle x\]
Now we have values of x and y
\[
   \Rightarrow \angle z = {30^ \circ } + {40^ \circ } \\
   \Rightarrow \angle z = {70^ \circ } \\
\]
Hence found the value of \[\angle z = {70^ \circ }\].

Note: Exterior angle of a triangle is at the outer part of a triangle formed at its vertex. The property of exterior angle is related with the sum of interior angles but remember the angles are opposite to external angles and not adjacent.