Question

If we have the vertices of a triangle as $A\left( 3,2,0 \right),B\left( 5,3,2 \right)$and $C\left( -9,6,-3 \right)$. If the bisector of $\angle A$ meets BC in D, then coordinates of D are\[\]
A. $\left( \dfrac{-19}{8},\dfrac{57}{16},\dfrac{17}{16} \right)$\[\]
B. $\left( \dfrac{19}{8},-\dfrac{57}{16},\dfrac{17}{16} \right)$\[\]
C. $\left( \dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right)$\[\]
D. $\left( -\dfrac{19}{8},\dfrac{57}{16},-\dfrac{17}{16} \right)$ \[\]

Answer 1

Hint: We find the length of the sides $AB$ and $AC$ using the distance formula in three dimensions. We use the angle bisector theorem and deduce that $D$ divides $BC$ at a ratio of $AB: AC$. We use the section formula for internal division find the coordinates of $D$ which divides $BC$ at $BD:CD=AB: AC$.\[\]

Complete step-by-step solution:
We know from section formula that any point $P(x,y,z)$ which divides a line segment internally $\overline{MN}$ in three dimensional space at a ratio $MP:PN=m:n$ with endpoints $M({{x}_{1}},{{y}_{1}},{{z}_{1}})\text{ and N(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{,}{{\text{z}}_{2}}\text{)}$ then the coordinates of P are given by
\[\begin{align}
  & x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n} \\
 & y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \\
 & z=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \\
\end{align}\]
The distance between two points in three dimensions with coordinates $M({{x}_{1}},{{y}_{1}},{{z}_{1}})\text{ and N(}{{\text{x}}_{2}}\text{,}{{\text{y}}_{2}}\text{,}{{\text{z}}_{2}}\text{)}$ is given by
\[MN=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\]
We know the "Angle Bisector" theorem says that an angle bisector of a triangle will divide the opposite side into two segments that are proportional to the other two sides of the triangle.\[\]
 

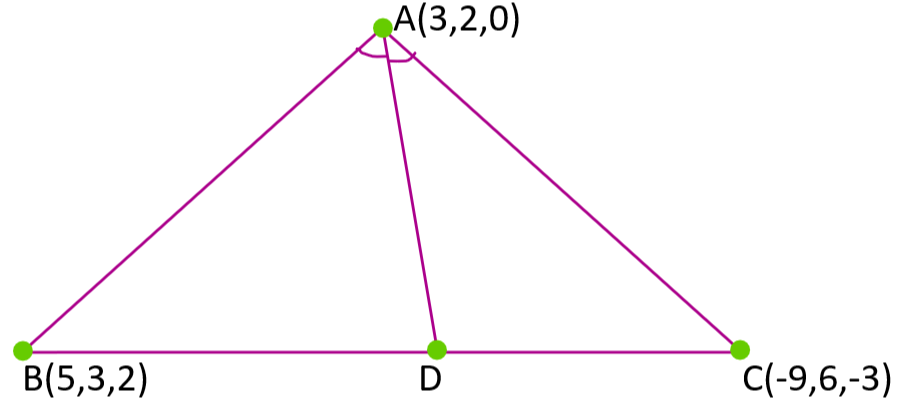
We have drawn the figure of the triangle as given in the question in three dimensional space whose vertices are $A\left( 3,2,0 \right),B\left( 5,3,2 \right)$ and $C\left( -9,6,-3 \right)$ . The internal angle bisector of angle $\angle A=\angle BAC$ meets the opposite side BC at the point D.
Let us find the length of the sides $AB$ and $AC$. We use the distance formula between two points in three dimensional spaces for $A\left( 3,2,0 \right)=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right), B\left( 5,3,2 \right)=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ and find the length of $AB$ as
\[AB=\sqrt{{{\left( 5-3 \right)}^{2}}+{{\left( 3-2 \right)}^{2}}+{{\left( 2-0 \right)}^{2}}}=\sqrt{4+4+1}=3\]
We again use the same distance formula for $C\left( -9,6,-3 \right)=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right),A\left( 3,2,0 \right)=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ and find the length of $AC$ as
\[AC=\sqrt{{{\left( -9-3 \right)}^{2}}+{{\left( 6-2 \right)}^{2}}+{{\left( -3-0 \right)}^{2}}}=\sqrt{144+16+9}=13\]
We use the angle bisector theorem and conclude that $D$ will divide the opposite $BC$ at a ratio of the other two sides $AB$ and $AC$. So we have
\[BD:CD=AB:AC=3:13\]
We use the section formula to find the coordinates of $D\left( x,y,z \right)$ which divide the line segment or side $BC$ with endpoints $B\left( 5,3,2 \right)=\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $C\left( -9,6,-3 \right)=\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ at a ratio $m:n=3:13$. The coordinates of $D$ are

\[\begin{align}
  & x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n}=\dfrac{3\left( -9 \right)+13\left( 5 \right)}{3+13}=\dfrac{38}{16}=\dfrac{19}{8} \\
 & y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}=\dfrac{3\left( 6 \right)+13\left( 3 \right)}{3+13}=\dfrac{57}{16} \\
 & z=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}=\dfrac{3\left( -3 \right)+13\left( 2 \right)}{3+13}=\dfrac{17}{16} \\
\end{align}\]
So we have the coordinates of point $D$ as $\left( \dfrac{19}{8},\dfrac{57}{16},\dfrac{17}{16} \right)$ and the correct option is C.

Note: We note that the question is silent about whether the triangle is acute or obtuse in angle. We have solved the problem assuming acute. If one of the angles $\angle B$ or $\angle C$ would have been obtuse then $D$ would have divided $BD$ externally and the coordinates of $D$ would have been $\left( \dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right)$