Question

If we have the vertices $A\left( -2,4 \right)$, $B\left( 0,0 \right)$ and $C\left( 4,2 \right)$ of a $\Delta ABC$, then find the length of the median through the vertex $A$.
(a) $2$
(b) $4$
(c) $3$
(d) $5$

Answer 1

Hint: For solving this question, first we will find the coordinates of the midpoint of the side BC with the help of the formula $D\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ . After that, we will find the distance between points $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ & $D\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ by distance formula, ${{d}_{AD}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ and select the correct option.

Complete step-by-step solution -
Given:
It is given that $A\left( -2,4 \right)$ , $B\left( 0,0 \right)$ and $C\left( 4,2 \right)$ are the vertices of $\Delta ABC$ and we have to find the length of the median through the vertex $A$ .
Now, we will use the following formulas of co-ordinate geometry to solve this question:
1. If $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ then, coordinates of the midpoint of segment AB will be $D\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ . This formula is also known as the midpoint formula.
2. Distance between points $A\equiv \left( {{x}_{1}},{{y}_{1}} \right)$ and $B\equiv \left( {{x}_{2}},{{y}_{2}} \right)$ is ${{d}_{AB}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ . This formula is also known as distance formula.
Now, let the median through vertex $A\left( -2,4 \right)$ intersect the side $BC$ at the point $D\left( h,k \right)$ . And as we know that, the median will intersect the side $BC$ at its midpoint so, we can say that, the point $D\left( h,k \right)$ will be the midpoint of the segment through points $B\left( 0,0 \right)$ & $C\left( 4,2 \right)$ .So, we can use the midpoint formula $D\equiv \left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ . Then,
$\begin{align}
  & h=\dfrac{{{x}_{_{1}}}+{{x}_{2}}}{2} \\
 & \Rightarrow h=\dfrac{0+4}{2} \\
 & \Rightarrow h=2 \\
 & k=\dfrac{{{y}_{_{1}}}+{{y}_{2}}}{2} \\
 & \Rightarrow k=\dfrac{0+2}{2} \\
 & \Rightarrow k=1 \\
\end{align}$
Now, from the above result, we conclude that the median through vertex $A\left( -2,4 \right)$ intersects the side $BC$ at the point $D\left( 2,1 \right)$ .
Now, we will use the distance formula ${{d}_{AD}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ to find the distance between points $A\equiv \left( -2,4 \right)$ and $D\equiv \left( 2,1 \right)$. Then,
$\begin{align}
  & {{d}_{AD}}=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} \\
 & \Rightarrow {{d}_{AD}}=\sqrt{{{\left( 2-\left( -2 \right) \right)}^{2}}+{{\left( 1-4 \right)}^{2}}} \\
 & \Rightarrow {{d}_{AD}}=\sqrt{{{\left( 2+2 \right)}^{2}}+{{\left( -3 \right)}^{2}}} \\
 & \Rightarrow {{d}_{AD}}=\sqrt{{{\left( 4 \right)}^{2}}+9} \\
 & \Rightarrow {{d}_{AD}}=\sqrt{16+9} \\
 & \Rightarrow {{d}_{AD}}=\sqrt{25} \\
 & \Rightarrow {{d}_{AD}}=\sqrt{{{5}^{2}}} \\
 & \Rightarrow {{d}_{AD}}=5 \\
\end{align}$
Now, from the above result, we conclude that the length of the median AD will be 5 units. For more clarity, look at the figure given below:

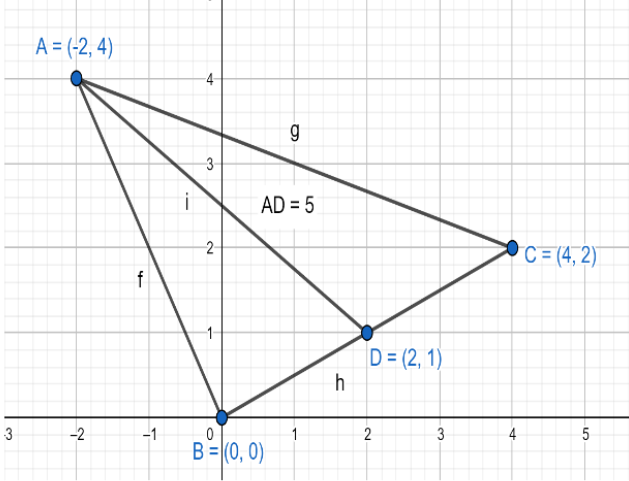
In the above figure, AD is the median on the side, BC from vertex A and its length is 5 units.
Hence, (d) will be the correct option.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. After that, we should solve stepwise and proceed as per the data given in the question. Moreover, we should use each formula with the correct values and take care of signs as well. Then, avoid calculation mistakes while solving to get the correct answer. And in the end, we should try to plot the given data on the graph and verify our answer.