Question

If we have a trigonometric ratio as \[\tan x = \dfrac{6}{8}\], how do you find \[\cos x\]?

Answer 1

Hint: Consider a right angled triangle with perpendicular length six units and base length eight units and then use Pythagoras theorem to evaluate the hypotenuse of the triangle.

Complete step-by-step solution:
Consider a right angled triangle \[ABC\] with right angle at \[\angle B\] and \[\angle C = x^\circ \].
It is known that the sum of all interior angles of a triangle is \[180^\circ \].
\[\angle A + \angle B + \angle C = 180^\circ \]
Substitute \[\angle B\] as \[90^\circ \] and \[\angle C\] as \[x\] degree to obtain the expression for \[\angle A\] as shown below.
\[ \Rightarrow \angle A + 90 + x = 180\]
\[ \Rightarrow \angle A = 90 - x\]
Therefore, the \[\angle A\] can be expressed as \[\left( {90 - x} \right)\] degree.
The right triangle \[ABC\] with right angle at \[\angle B\], \[\angle C = x\] and so \[\angle A = 90 - x\] is shown in the figure below.

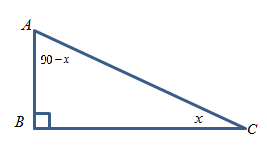
Now, use the definition of trigonometric ratio for \[\tan x\].
For an angle \[x\] as argument, side \[AB\] act as perpendicular (side in front of the argument angle), side \[BC\] act as base and side \[AC\] always be hypotenuse for this triangle.
The trigonometry ratio \[\tan x\] is defined as the ratio of perpendicular to the base with respect to angle \[x\].
\[\tan x = \dfrac{P}{B}\]
\[ \Rightarrow \tan x = \dfrac{{AB}}{{BC}}\]
As it is given in the question that \[\tan x = \dfrac{6}{8}\], it implies that the ratio of side \[AB\] to side \[BC\] is \[6:8\].
So, we can consider the length of side \[AB\] as \[6l\] and side \[BC\] as \[8l\].
Use Pythagoras theorem to evaluate the hypotenuse of the triangle as shown below.
\[A{B^2} + B{C^2} = A{C^2}\]
Substitute length of \[AB\] as \[6l\] and length of \[BC\] as \[8l\] to calculate the length of side \[AC\] as shown below.
\[ \Rightarrow {\left( {6l} \right)^2} + {\left( {8l} \right)^2} = A{C^2}\]
\[ \Rightarrow 36{l^2} + 64{l^2} = A{C^2}\]
\[ \Rightarrow 100{l^2} = A{C^2}\]
\[ \Rightarrow {\left( {10l} \right)^2} = A{C^2}\]
Thus, the length of the side \[AC\] is \[10l\].
Now, calculate the trigonometry ratio \[\cos x\] by the use of definition that it is the ratio of base to the hypotenuse with respect to angle \[x\].
\[\cos x = \dfrac{B}{H}\]
\[ \Rightarrow \cos x = \dfrac{{BC}}{{AC}}\]
Substitute the length of side \[BC\] and \[AC\] in the above equation and solve further as shown below.
\[ \Rightarrow \cos x = \dfrac{{8l}}{{10l}}\]
\[ \Rightarrow \cos x = \dfrac{8}{{10}}\]
\[ \Rightarrow \cos x = \dfrac{4}{5}\]
Thus, the value for \[\cos x\] is \[\dfrac{4}{5}\], if the value for \[\tan x\] is \[\dfrac{6}{8}\].

Note: The perpendicular side and base side in a right angled triangle is defined with respect to one of the acute angles from the given triangle but hypotenuse is the same for both acute angles (longest side of a triangle or side opposite to the right angle).