Question

If we are given two variables as $a=\cos 2\text{ }$ and $b=\sin 7$ then
A. $a>0,b>0$
B. $ab>0$
C. $a\text{<}b$
D. $a\text{>}b$

Answer 1

Hint: We need to find the relation between $a\text{ and }b$ . First, plot the graph of $\sin \theta $ and $\cos \theta $ in a single graph. Then locate $\cos 2\text{ }$ and $\sin 7$ . From the resulting graph, we will get the correct option. Or by evaluating each option, we can conclude a single option.

Complete step-by-step solution
We need to find the relation between $a\text{ and }b$ .
First, let us plot the graph of $\sin \theta $ and $\cos \theta $ .

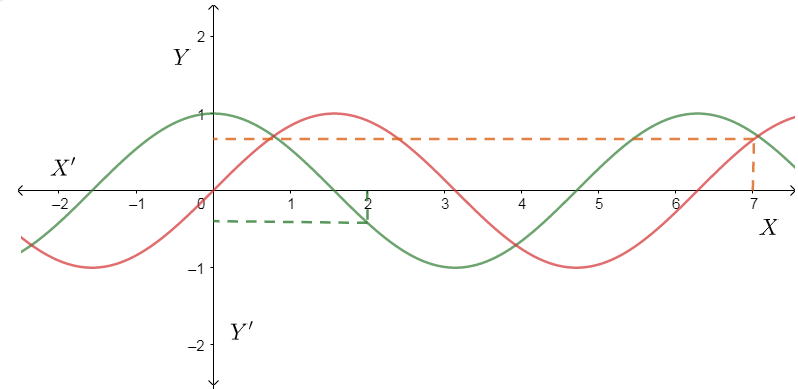
The red colour shows $\sin \theta $ and the green colour denotes $\cos \theta $ .
In the graph, we have located $\cos 2\text{ }$ that is marked in the green dotted line. This value falls in the negative wave of $\cos \theta $ or in other words, this corresponds to a negative value. Hence $\cos 2 < 0$ .
$\sin 7$ is denoted as a red dotted line in the graph that falls on the positive wave. That is, its value is positive. Hence this can be shown as $\sin 7>0$.
Now let us evaluate each option.
Option A shows that $a>0,b>0$ . This cannot be true as $\cos 2 < 0$ and $\sin 7>0$ .
Option B. shows that $ab>0$ . Clearly, this is false.
Option C has $a\text{<}b$ . This is true as $\cos 2\text{ }$ is negative and $\sin 7$ is positive.
Option D shows that $a\text{>}b$ . Obviously, this is false.
Hence, the correct option is C.

Note: Apart from the given options, there is also another possibility. As $\cos 2 < 0$ and $\sin 7>0$ , when we evaluate $ab$ , that is, $\cos 2\text{ }\times \sin 7=-ve\times +ve=-ve$ . Thus $ab>0$ . So there can be an error when evaluating option B.