Question

If ${w_1},\,{w_2},\,{w_3}$ and ${w_4}$are work done in isothermal, adiabatic, isobaric and isochoric reversible processes, respectively then the correct sequence (for expansion) would be:

A. ${w_1} < \,{w_2} < \,{w_3}\, < \,{w_4}$
B. ${w_1} = {w_2} = \,{w_3}\, = {w_4}$
C. ${w_3} < \,{w_2} < \,{w_4}\, < \,{w_1}$
D. ${w_3} > \,{w_1} > \,{w_2}\, > \,{w_4}$

Answer 1

Hint: Work is the product of pressure and volume. A curve between pressure and volume is plotted to determine the work done. The amount of work done depends upon the area under the curve.

Complete step by step answer:
Suppose an ideal gas is taken in a cylinder having a moving piston. When a gas expands at a constant temperature the volume of the gas increases. The piston moves upward. The gas does some work for this expansion.
The expression of work done in a reversible expansion of an ideal gas gives the work done during the change from initial to a final volume.
The formula of work is as follows:
$W = - PdV$
Where,
$W$ is the work done.
$P$is pressure.
$dV$is the volume change.
To determine the total change, integrate the work formula from initial volume ${V_i}$ to final volume${V_f}$.
$W = - P\int\limits_{{V_I}}^{{V_f}} {dV} $
So, the work done depends upon the pressure and change in volume. More will be the change in volume, more will be the work.
The pressure and volume curve is plotted to determine the work done. Volume is taken on x-axis and pressure is taken on y-axis. The area under the curve denotes the work done.
More will be the area under the curve more will be the work done.
The pressure-volume curve for isothermal, adiabatic, isobaric and isochoric reversible expansion processes, is as follows:

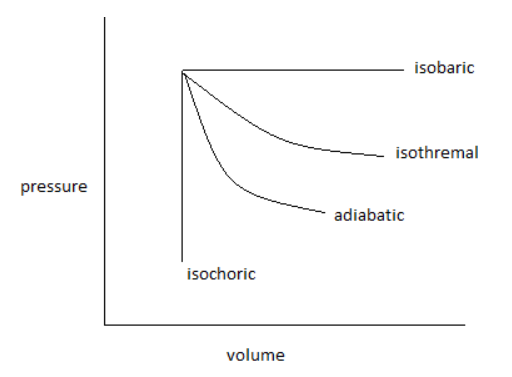
From the curve, it is clear that more area is covered by the isobaric reversible expansion process and the minimum area is covered by the isochoric reversible expansion process.
So, the decreasing order of area covered by each process is as follows:
Isobaric > Isothermal > Adiabatic > Isochoric.
So, the decreasing order of work done in each reversible expansion process is as follows:
${w_3} > \,{w_1} > \,{w_2}\, > \,{w_4}$
So, the correct sequence (for expansion) would be ${w_3} > \,{w_1} > \,{w_2}\, > \,{w_4}$.

Therefore, option (D) ${w_3} > \,{w_1} > \,{w_2}\, > \,{w_4}$ is correct.

Note:
Area under the pressure-volume curve is directly proportional to the work done. In the isochoric reversible expansion process, the volume is constant so, the change in volume during the process is zero. The work done in the isochoric process is zero. In the isothermal process, the heat is given by surrounding for work done whereas the heat change is zero in the adiabatic process so, the work done in the isothermal process is greater than the work done in the adiabatic process.