Question

If v stands for the velocity of sound, E is elasticity and d the density, then find $x$ in the equation $v = {\left( {D/E} \right)^x}$
A. 1
B. 0.5
C. -1
D. -0.5

Answer 1

Hint: Here, we need to understand the concept of Bulk Modulus. Bulk Modulus is an indication of the compressibility of the material, wherein it represents the change in volume by application of uniform pressure from all sides.

Complete step by step answer:
The mathematical expression for Bulk’s Modulus is given by –
$K = - \dfrac{{dP}}{{dV/V}}$
where $dP$= change in the pressure and $dV/V$ is the change in volume per the original volume
The speed of sound in a medium depends mainly on the stiffness of the medium. The stiffness is represented by different moduli of elasticity in different media i.e. in the solids, it is the Young’s Modulus and in liquid and gases, it is the Bulk’s Modulus. These moduli are an indication of a property of the material called stiffness, which means the resistance of the material to change when it is subjected to change in the material such as application of force or pressure.
There are two types of waves, namely, longitudinal and transversal. In longitudinal waves, the particles vibrate in the same direction as that of the direction of propagation and in the case of transverse waves, the particles vibrate in the perpendicular directions.

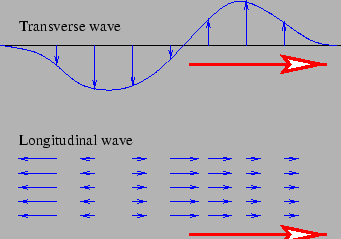
The sound waves are longitudinal in nature in fluids. Hence, there is an application of pressure on the air column. Whenever there is pressure applied to the air, there is a change in the volume. Thus, you can see that we are coming to an understanding that the speed of sound is dependent on the bulk modulus in fluids.
The equation which gives the relation is called Newton-Laplace equation, which states that
Speed of sound, $v = \sqrt {\dfrac{K}{\rho }} $
where K = bulk modulus of elasticity and $\rho $= density of the fluid.
Now, substituting K = E and $\rho = D$ as per the given question, we have –
\[
  v = \sqrt {\dfrac{K}{\rho }} \\
  v = \sqrt {\dfrac{E}{D}} \\
  v = {\left( {\dfrac{E}{D}} \right)^{0.5}} = {\left( {\dfrac{D}{E}} \right)^{ - 0.5}} \\
 \]
By comparing to ${\left( {\dfrac{D}{E}} \right)^x}$in the question, we get –
$x = - 0.5$

$\therefore $ $x = - 0.5$. Hence, the correct option is Option D.

Note:
Since the speed of the sound in fluids depends on the density, this is the main reason why the speed of sound varies along with the temperature of the fluid.
$
v = \sqrt {\dfrac{K}{\rho }} \\
\Rightarrow v \propto \dfrac{1}{{\sqrt \rho }} \\
 $
As per the Gas Laws, we have $T \propto \rho $, we get,
$v \propto \dfrac{1}{{\sqrt T }}$
So, the velocity of sound in fluids is inversely proportional to the square root of the temperature of the fluid.