Question

If V is the volume of parallelepiped formed by the vectors\[\overrightarrow{a}\,,\,\overrightarrow{b\,},\,\overrightarrow{c}\]as three coterminous edges is 27 cubic units, then the volume of parallelepiped having \[\overrightarrow{\alpha }=\overrightarrow{a}+2\,\overrightarrow{b\,}-\,\overrightarrow{c}\], \[\overrightarrow{\beta }=\overrightarrow{a}-\,\overrightarrow{b\,}+0\,\overrightarrow{c}\]and \[\overrightarrow{\gamma }=\overrightarrow{a}-\,\overrightarrow{b\,}-\overrightarrow{c}\] as three coterminous edges is?
A) 27
B) 9
C) 81
D) 48

Answer 1

Hint: We will calculate the required volume of the parallelepiped using the volume V of the given parallelepiped. Volume of the parallelepiped is given as: \[27\]cubic units. Whereas \[\overrightarrow{a}\,,\,\overrightarrow{b\,},\,\overrightarrow{c}\] as three edges of parallelepiped. We have the formula of volume of parallelepiped \[V=\dfrac{1}{6}\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]\]. In question that is \[V=\dfrac{1}{6}\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]=27\] from this equation we have to find the required volume that is \[V=\dfrac{1}{6}\left[ \overrightarrow{\alpha }\,\,\overrightarrow{\beta \,}\,\overrightarrow{\gamma } \right]\].

Complete step by step answer:
We are given that the volume of the parallelepiped having three coterminous edges \[\overrightarrow{a}\,,\,\overrightarrow{b\,\,\,}\text{and}\,\,\,\overrightarrow{c}\] is: V

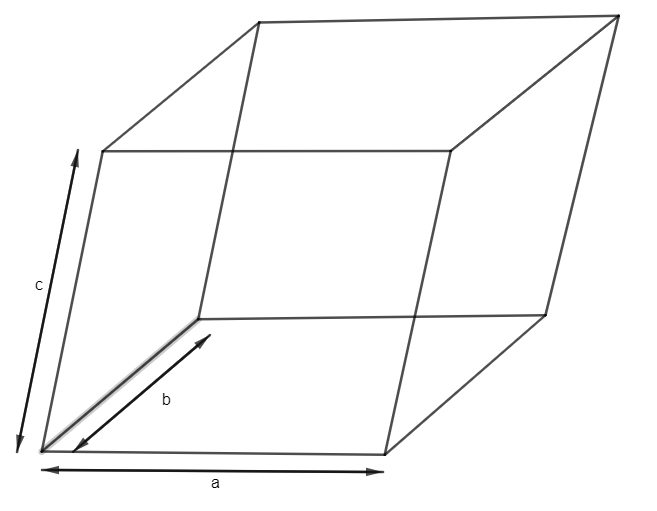
We need to find the volume of the parallelepiped having three coterminous edges as:
\[\overrightarrow{\alpha }=\overrightarrow{a}+2\,\overrightarrow{b\,}-\,\overrightarrow{c}\]
\[\overrightarrow{\beta }=\overrightarrow{a}-\,\overrightarrow{b\,}+0\,\overrightarrow{c}\]
\[\overrightarrow{\gamma }=\overrightarrow{a}-\,\overrightarrow{b\,}-\overrightarrow{c}\]
We know that the formula of the parallelepiped is given by the formula
According to the given question is that
\[V=\dfrac{1}{6}\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]=27\]
The required volume of the parallelepiped is given by
\[V=\dfrac{1}{6}\left[ \overrightarrow{\alpha }\,\,\overrightarrow{\beta \,}\,\overrightarrow{\gamma } \right]\]
Substituting the value of\[\overrightarrow{\alpha }\,\], \[\overrightarrow{\beta \,}\]and \[\,\overrightarrow{\gamma }\] in the above equation we get:
\[V=\dfrac{1}{6}\left[ \overrightarrow{a}+2\,\overrightarrow{b\,}-\,\overrightarrow{c}\,\,\overrightarrow{a}-\,\overrightarrow{b\,}+0\,\overrightarrow{c}\,\,\,\overrightarrow{a}-\,\overrightarrow{b\,}-\overrightarrow{c} \right]--(1)\]
But, \[\left[ \overrightarrow{a}+2\,\overrightarrow{b\,}-\,\overrightarrow{c}\,\,\overrightarrow{a}-\,\overrightarrow{b\,}+0\,\overrightarrow{c}\,\,\,\overrightarrow{a}-\,\overrightarrow{b\,}-\overrightarrow{c} \right]=\left| \begin{matrix}
   \overrightarrow{a} & 2\,\overrightarrow{b\,} & -\,\overrightarrow{c} \\
   \overrightarrow{a} & -\,\overrightarrow{b\,} & 0\,\overrightarrow{c} \\
   \,\overrightarrow{a} & -\,\overrightarrow{b\,} & -\overrightarrow{c} \\
\end{matrix} \right|--(2)\]
Or, it can be also written by using the identity \[\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]=\left| \begin{matrix}
   x & y & z \\
   m & n & o \\
   \,p & q & r \\
\end{matrix} \right|\] where, \[\overrightarrow{a}=x\widehat{i}+y\widehat{j}+z\widehat{k}\]
\[\overrightarrow{b}=m\widehat{i}+n\widehat{j}+o\widehat{k}\]
\[\overrightarrow{c}=p\widehat{i}+q\widehat{j}+r\widehat{k}\]
Now, the equation\[(2)\]can be written as \[\left[ \overrightarrow{a}+2\,\overrightarrow{b\,}-\,\overrightarrow{c}\,\,\overrightarrow{a}-\,\overrightarrow{b\,}+0\,\overrightarrow{c}\,\,\,\overrightarrow{a}-\,\overrightarrow{b\,}-\overrightarrow{c} \right]=\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]\]
Substitute this equation in equation (1)
\[V=\dfrac{1}{6}\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]\]
From this this equation\[V=\dfrac{1}{6}\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]=27\]
We get this value \[\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]=27\times 6\]
Now substitute this value in \[V=\dfrac{1}{6}\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|\left[ \overrightarrow{a}\,\,\overrightarrow{b\,}\,\overrightarrow{c} \right]\]we get:
\[V=\dfrac{1}{6}\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|\times 27\times 6\]
Here 6 gets cancelled us we get:
\[V=\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|\times 27\]
Now we have to take the determinant that is \[\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|=1(1-0)-2(-1-0)-1(-1+1)\]
By simplifying this we get:
\[\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|=3\]
Substitute the value in \[V=\left| \begin{matrix}
   1 & 2 & -\,1 \\
   1 & -\,1 & 0\, \\
   1 & -\,1 & -1 \\
\end{matrix} \right|\times 27\]we get:
\[V=3\times 27\]
By simplifying we get:
\[V=81\]
Volume of the required parallelepiped is 81 cubic units. So, option (C) is correct.

Note:
There might be a chance of getting confused while solving the box product and you must be careful while using the identity to simplify the required volume of the given parallelepiped. You may also solve this question by simplifying the volume using the formula of calculating the area of the cross product or by using the identities of matrices.