Question

If two zeroes of the polynomial $P\left( x \right)={{x}^{3}}+2{{x}^{2}}-9x-18$ are $3$ and $-3$ , then find the other zero of the polynomial $P\left( x \right)$.

Answer 1

Hint: For the polynomial, we are given that out of the three roots, two of the roots are $3$ and $-3$ . We need to find out the third root. This will be done by dividing the polynomial by the quadratic expression ${{x}^{2}}-9$ . This gives the linear expression $x+2$ . From this, we can get the third root.

Complete step-by-step solution:
A polynomial is an expression of more than two algebraic terms. A polynomial when equated to some constant is called an equation. The given polynomial that we have in our problem is,
$P\left( x \right)={{x}^{3}}+2{{x}^{2}}-9x-18$
If we equate this to zero, then we get the equation ${{x}^{3}}+2{{x}^{2}}-9x-18=0$ . The solutions of this equation are called the roots of the polynomial. It is given that out of the three roots, two of the roots are $3$ and $-3$ . This means that the factors of the polynomial ${{x}^{3}}+2{{x}^{2}}-9x-18$ will be $x-3$ and $x+3$ . The polynomial ${{x}^{3}}+2{{x}^{2}}-9x-18$ can be written as $\left( x-3 \right)\left( x+3 \right)\left( x-a \right)$ , where “a” is the third root. $\left( x-3 \right)\left( x+3 \right)$ is ${{x}^{2}}-9$ . Dividing the polynomial by ${{x}^{2}}-9$ gives
\[\begin{align}
  & ~~~~~~~~~~x+2 \\
 & {{x}^{2}}-9\left| \!{\overline {\,
 \begin{align}
  & {{x}^{3}}+2{{x}^{2}}-9x-18 \\
 & {{x}^{3}}~~~~~~~~~~-9x \\
\end{align} \,}} \right. ~ \\
 & {{x}^{2}}-9\left| \!{\overline {\,
 \begin{align}
  & 2{{x}^{2}}~~~~~~~~~~-18 \\
 & 0 \\
\end{align} \,}} \right. \\
\end{align}\]
$x+2$ as the quotient. This means that $x+2$ is the third factor and $-2$ is the third root.
Therefore, we can conclude that the other root of the polynomial is $-2$.

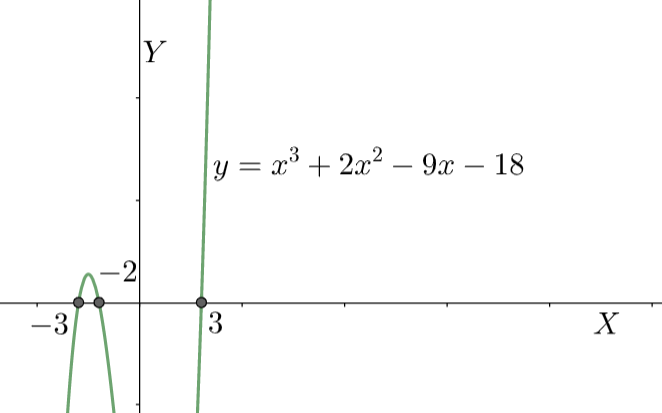
Note: We can solve the problem in another way. If we draw the graph of the equation ${{x}^{3}}+2{{x}^{2}}-9x-18=0$ , then we get all the roots. The points on the x-axis where the curve cuts the x-axis will be the roots of the polynomial. We see that the three roots are $3,-3,-2$ .