Question

If two sides and median bisecting one of these sides of a triangle are respectively proportional to the two sides and the corresponding median of another triangle then prove that the triangles are similar.

Answer 1

Hint:In $\Delta ABC$, extend AD to E and join thus getting a parallelogram ABEC. Similarly extend PM to N and get parallelogram PQNR. Thus, prove that $\Delta ABE\sim \Delta PQN,\Delta ACE\sim \Delta PRN$. Thus prove $\Delta BAC=\Delta QPR$. Hence by SAS similarly they will be equal.

Complete step-by-step answer:
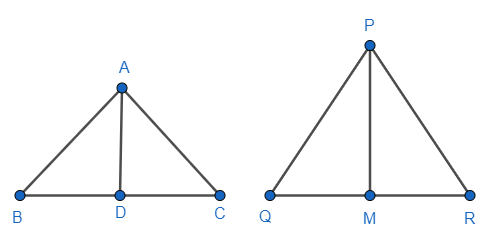
We have been given two triangles ABC and PQR. Now from the triangle we can say that AD and PM are their median. Now we have been told that 2 sides and median AD triangle ABC is proportional to 2 sides and median PM of triangle PQR. Hence, we have to prove that $\Delta ABC=\Delta PQR$
Let us consider that AB and PQ are proportional and AC and PR is proportional from $\Delta ABC,\Delta PQR$. Thus, we can write that
$\dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{AD}{PM}$ …………….. (i)
Now let us produce AD to E, such that AD = DE. Similarly produce PM to N in $\Delta PQR$, such that
PM = NN.
Now join BE, CE, QN, RN as shown in the figure.

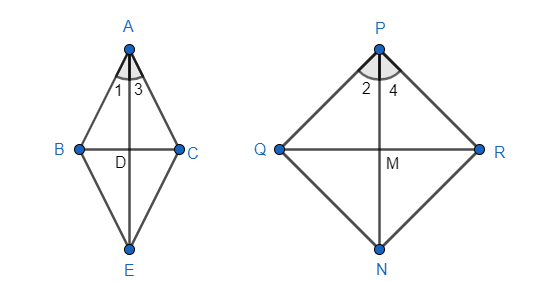
Thus, we get a quadrilateral ABEC and PQNR. They are parallelogram because their diagonals bisect each other at point D and M.
Now consider parallelogram ABEC and PQNR BE = AC and QN = PR, opposite sides of the parallelogram are equal. Hence, we can write it as,
$\dfrac{BE}{AC}=1,\dfrac{QN}{PR}=1$
Now from the above we can say that, $\dfrac{BE}{AC}=\dfrac{QN}{PR}$
We can cross-multiply them to get,
 $\dfrac{BE}{QN}=\dfrac{AC}{PR}$
From equation (i) we have $\dfrac{AB}{PQ}=\dfrac{AC}{PR}$
Hence comparing both we can say that $\dfrac{BE}{QN}=\dfrac{AB}{PQ}$
$\therefore \dfrac{AB}{PQ}=\dfrac{BE}{QN}$………………. (ii)
We said that AD = DE
Hence AE = AD + DE = AD + AD = 2AD
i.e., AE = 2AD.
Similarly, PM = MN
$\therefore $ PN = PM + MN –PM + PM = 2PM
i.e., PN = 2PM
Now from equation (i) $\dfrac{AB}{PQ}=\dfrac{AD}{PM}$
Multiply 2 $\left( \dfrac{AD}{PM} \right)$ on both numerator and denominator
$\therefore \dfrac{AB}{PQ}=\dfrac{2AD}{2PM}=\dfrac{AE}{PN}$ $\because $ AE = 2AD ,PN = 2PM
i.e., $\dfrac{AB}{PQ}=\dfrac{AE}{PN}$ ………………..(iii)
from equation (ii) and (iii)
$\begin{align}
  & \dfrac{AB}{PQ}=\dfrac{BE}{QN},\dfrac{AB}{PQ}=\dfrac{AE}{PN} \\
 & \therefore \dfrac{BE}{QN}=\dfrac{AE}{PN} \\
\end{align}$
From the above we can say that $\Delta ABE\cong \Delta PQN$ as two sides of $\Delta ABE$ is proportional to $\Delta PQN$. Hence the corresponding angles of 2 triangles are equal.
$\therefore \angle 1=\angle 2$ ……………. (iv)
Similarly, we can prove that $\Delta ACE\sim \Delta PRN$.
Hence from this we can say that $\angle 3=\angle 4$ ……………. (v)
Now let us add (iv) and (v) we get
$\angle 1+\angle 3=\angle 2+\angle 4$
From the figure you get $\angle BAC=\angle 1+\angle 3,\angle PQR=\angle 2+\angle 4$
$\therefore \angle BAC=\angle QPR$
And from equation (i) $\dfrac{AB}{PQ}=\dfrac{AC}{PR}$
$\therefore \Delta ABC\sim \Delta PQR$, by SAS similarity criterion.
i.e., 2 sides and one angle of $\Delta ABC$ is equal angle and 2 sides of $\Delta PQR$
Hence $\Delta ABC\sim \Delta PQR$.
Thus, we proved that both angles are similar.

Note: You should know the basic properties of triangles and parallelograms to solve a particular question like this. The entire question is based on their property. It is given 3 sides are proportional, you make think of moving I using SSS criterion, but that won’t be correct. Use SAS.