Question

If two numbers are in the ratio 6:13 and their LCM is 312, find the numbers.

Answer 1

Hint: First of all, assume two numbers as 6x and 13x where x is the common multiple of two numbers. Now, equate \[6\times 13\times x\] to LCM that is 312 to find the value of x and from that find the value of two numbers.

Complete step-by-step answer:
In this question, we are given that if two numbers are in the ratio 6:13 and their LCM is 312, then we have to find these numbers. Before proceeding with the question, let us see what LCM is and how to find it.
LCM: LCM is the least common multiple of the given numbers or in other words, we can say that it is the smallest positive integer that is divisible by the given numbers. The LCM of two or more prime numbers is always equal to the product of these numbers. For example, if we have 6, 8, 10, we get the LCM as follows:
\[6=2\times 3\]
\[8=2\times 2\times 2={{2}^{3}}\]
\[10=2\times 5\]
So, we get the LCM of 6, 8, and 10 by multiplying the highest power of each factor that is \[{{2}^{3}}.5.1=120\].
Now, let us consider our question. We are given two numbers that are in the ratio of 6:13. So, let us consider two numbers as 6x and 13x where x is the common multiple.
We can write 6x = 2. 3. x and 13x = 13.x
Here, we can see that the highest powers of the various factor is 1 that is \[{{2}^{1}},{{3}^{1}},{{13}^{1}},{{x}^{1}}.\]
So, we get the LCM of 6x and 13x as 2.3.13.x = 78x…..(i)
We are also given the LCM of 6x and 13x is 312. So, by equating the value of LCM in equation (i) with 312, we get,
\[78x=312\]
\[x=\dfrac{312}{78}\]
\[x=4\]
So, we get the first number as 6x = 6.4 = 24 and the second number as 13x = 13.4 = 52.

Note: In this question, many students write the LCM of 6x and 13x as \[6x.13x=78{{x}^{2}}\] which is wrong because \[{{x}^{2}}\] is not coming in any of the numbers but the only x is coming, so the highest power of x is 1. Here, LCM would be 6.13.x = 178x. Also, students can cross-check their answer by finding the LCM of the number 24 and 52 and checking if it is equal to 312 or not as follows:
We can use the prime factorization method to get the LCM of 24 and 52 as follows:

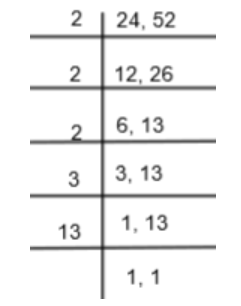
So, we get the LCM as \[2\times 2\times 2\times 3\times 13=312\] which is equal to the value. So, our answer is correct.