Question

If two lines intersect at a point to form four angles and one angle is twice as large as its adjacent (neighboring) angle, what is the degree measure of the smallest angle? (in degrees)

Answer 1

Hint: To obtain the degree measure of the smallest angle we will use the concept of sum of all angles in a straight line. Firstly by using the information we will draw the diagram then we will let one angle among them as $x$ and adjacent angle to it as $2x$. Then we will use the concept that the sum of all angles in a straight line is ${{180}^{\circ }}$ and then find the smallest among them.

Complete step by step solution:
The information is given as If two lines intersect at a point to form four angles and one angle is twice as large as its adjacent (neighboring) angle then we have to find the smallest angle.
Firstly we will draw the two lines $AB$ and $CD$ such that when they intersect four angles are formed.

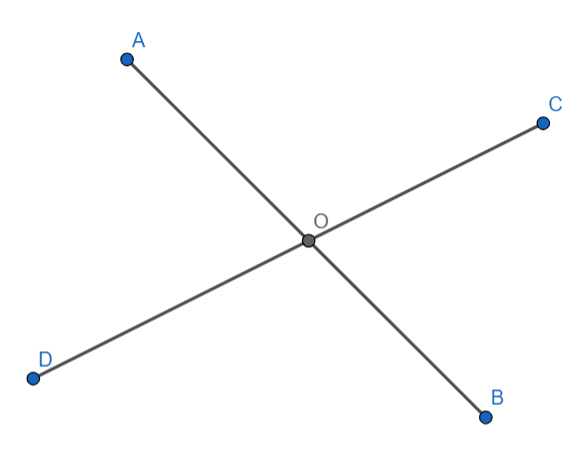
So we get the above diagram where the center is at $O$
Now, let
$\angle BOC=x$….$\left( 1 \right)$
So the angle adjacent to it will be twice of it as:
$\angle BOD=2x$…..$\left( 2 \right)$
We know that the sum of all angles on a straight line is ${{180}^{\circ }}$.
So
$\angle COD={{180}^{\circ }}$…..$\left( 3 \right)$
Also we know that
$\angle BOD+\angle BOC=\angle COD$
On substituting value from equation (1)-(3) in above equation and simplifying it we get,
$\begin{align}
  & \Rightarrow 2x+x={{180}^{\circ }} \\
 & \Rightarrow 3x={{180}^{\circ }} \\
 & \Rightarrow x=\dfrac{{{180}^{\circ }}}{3} \\
 & \therefore x={{60}^{\circ }} \\
\end{align}$
On putting the above value in equation (1) and (2) we get,
$\angle BOC={{60}^{\circ }}$
$\angle BOD={{120}^{\circ }}$
Now as pair of vertical opposite angles is equal so,
 $\begin{align}
  & \angle AOD=\angle BOC \\
 & \angle AOD={{60}^{\circ }} \\
\end{align}$
And
$\begin{align}
  & \angle AOC=\angle BOD \\
 & \angle AOC={{120}^{\circ }} \\
\end{align}$
So the smallest angle obtained is ${{60}^{\circ }}$
Hence if two lines intersect at a point to form four angles and one angle is twice as large as its adjacent (neighboring) angle the degree measure of the smallest angle is ${{60}^{\circ }}$

Note: When two lines intersect each other the opposite angles formed is known as vertical angles. The value of angle can be anything where the vertical angle has a common vertex. The point at which the two lines intersect is known as the point of Intersection.