Question

If two lines are parallel, we can conclude that:
A). Alternate angles are equal
B). Corresponding angles are equal
C). Co-interior angles are supplementary
D). All of the above

Answer 1

Hint: In this question first of all we have to know about the meaning of parallel lines. First define the terms Alternate angles, Corresponding angles, Co interior angles and supplementary angles. Then we have to analyse the given option by using the properties of parallel lines. We select those options which are in accordance with the properties of parallel lines.

Complete step-by-step answer:
First of all, we draw two parallel lines ${A}'A$ and ${B}'B$ and one transversal line ${C}'C$, which intersect line${A}'A$ and Line ${B}'B$.

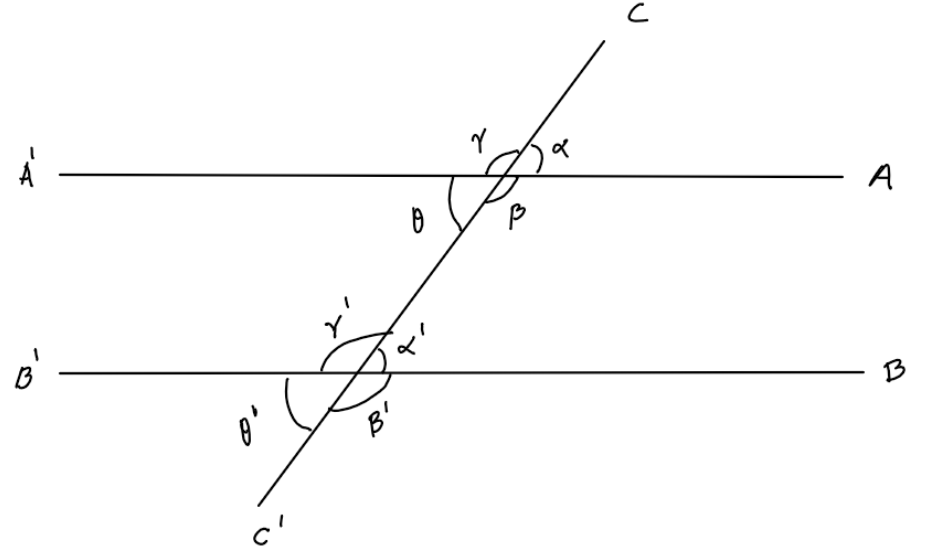
Alternate angle:
Alternate angles are the angles that are in the opposite position relative to a transversal intersecting two lines.
In the figure $\theta \text{ and }{\alpha }'$are alternate angles.
Corresponding angles:
Corresponding angles are the angles in matching corners when a transversal line intersects two parallel lines.
In figure $\alpha \text{ and }{\alpha }'$ are corresponding angles.
When two parallel lines are intersected by a transversal line then corresponding angles are equal. This is a postulate. Hence, option B is correct.
Co-interior angles
Co-interior angles lie between two lines and on the same side of a transversal line.
In figure $\alpha \text{ and }\beta $ are co-interior angles.
Now from figure we have
$\alpha +\beta =180{}^\circ $
As both angles are made on a straight line.
Hence $\alpha \text{ and }\beta $are supplementary angles. So, option C is correct.
As we can write
$\alpha +\gamma =180{}^\circ =\gamma +\theta $
So, we can write
$\alpha =\theta $
Similarly, we can write
$\begin{align}
  & \gamma =\beta \\
 & {\alpha }'={\theta }' \\
 & {\gamma }'={\beta }' \\
\end{align}$
That is, vertically opposite angles are equal.
As we see above
$\alpha \text{ = }{\alpha }'$
$\alpha =\theta $
So, we can write
$\theta ={\alpha }'$
Hence, alternate angles are equal. So, option A is correct.
So, our option D is also correct.
Hence, we mark option D as the correct answer.

Note: It should be noted that the sum of angles of a straight line is$180{}^\circ $.
A postulate refers to a hypothesis specific to a certain line of inquiry, that was accepted without proof. An axiom is a self- evident truth.