Question

If two interior angles on the same side of transversal intersecting two parallel lines are in the ratio 3:7, the measure of the larger angle is

Answer 1

Hint: : In this question we are asked to find the longer angle between interior angles. We have two interior angles on the same side of the transversal intersecting two parallel lines. As the ratio is given in the problem, we have to consider a fixed variable $x$. Then the interior angles become $3x$ and $7x$. We all know that the sum of interior angles on the same side of the transversal is ${180^ \circ }$.
We have to sum up the interior angles and equate it to ${180^ \circ }$ and then simplify the equation to get the value of $x$. After getting the value of $x$, we have to substitute the value of $x$ in the values of interior angles then we can find out the longer angle between the two interior angles.

Complete step-by-step solution:

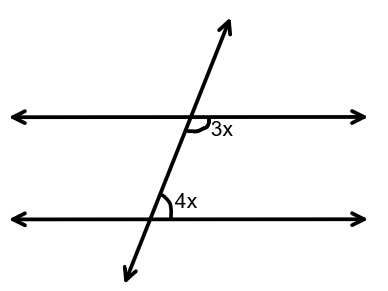
Let us consider a fixed variable$x$.
Then the values of two interior angles of the same side of transversal becomes $3x$ and$7x$.
We know that $3x + 7x = {180^ \circ }$
$3x + 7x = {180^ \circ } \\
\Rightarrow 10x = {180^ \circ } \\
\Rightarrow x = \dfrac{{{{180}^ \circ }}}{{10}} \\
\Rightarrow x = {18^ \circ } $
Hence $x = {18^ \circ }$
The values of interior angles on the same side of transversal are
$3x = 3 \times {18^ \circ } \\
\Rightarrow 3x = {54^ \circ } $
$\Rightarrow 7x = 7 \times {18^ \circ } \\
\Rightarrow 7x = {126^ \circ } $
So the longer angle is ${126^ \circ }$.

Note: When a pair of parallel lines are intersected by a transversal, the interior angles are equal to their alternate angles. These pairs are termed as alternate interior angles. We also get several pairs when a transversal intersects a pair of parallel lines which are redundant to this question so let us limit ourselves here for this question.