Question

If two distinct chords of parabola \[{{y}^{2}}=4ax\], passing through \[\left( a,2a \right)\] are bisected on the line \[x+y=1\], then the length of latus rectum is
(a) 2
(b) 1
(c) 4
(d) 5

Answer 1

Hint: The figure showing the given data is

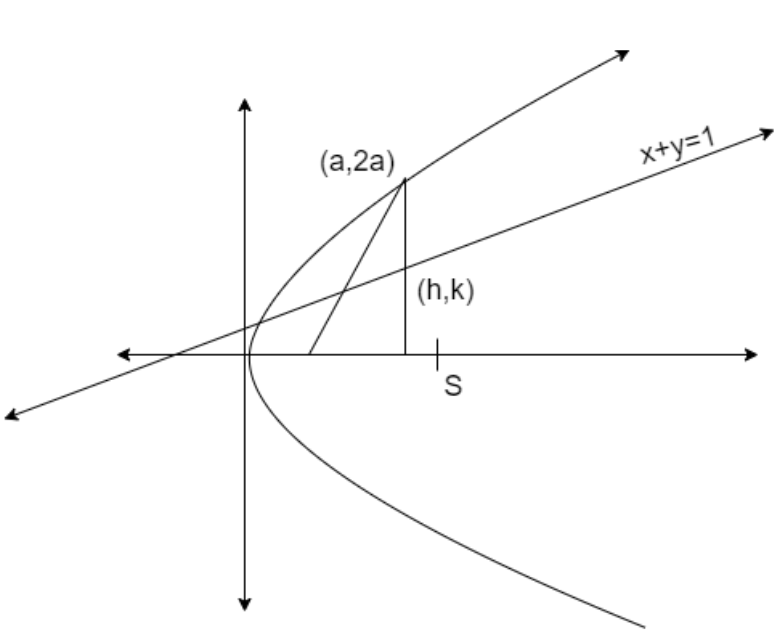
We solve this problem by assuming the mid - point as \[\left( h,k \right)\] that lies on the line \[x+y=1\]. Then we use the formula of the line equation having the mid – point of a curve \[S\]that is \[{{S}_{1}}={{S}_{11}}\]. If \[S\equiv {{y}^{2}}-4ax=0\] then the representation \[{{S}_{1}},{{S}_{11}}\] with respect to point \[\left( {{x}_{1}},{{y}_{1}} \right)\] is given as
\[\Rightarrow {{S}_{1}}=y{{y}_{1}}-2a\left( x+{{x}_{1}} \right)\]
\[\Rightarrow {{S}_{11}}={{y}_{1}}^{2}-4a{{x}_{1}}\]
By using the above results we find the range of \['a'\] to get the latus rectum as \['4a'\]

Complete step-by-step solution:
Let us assume that the point at which the chords are bisected as \[\left( h,k \right)\]
We are given that the chords are bisected on the line \[x+y=1\]
We know that the point \[\left( h,k \right)\] satisfies the equation \[x+y=1\]
Now, by substituting the point in the line we get
\[\begin{align}
  & \Rightarrow h+k=1 \\
 & \Rightarrow k=1-h \\
\end{align}\]
So, we can take the mid – point as \[\left( h,1-h \right)\]
We know that the formula of line equation having mid – point of a curve \[S\] that is \[{{S}_{1}}={{S}_{11}}\].
If \[S\equiv {{y}^{2}}-4ax=0\] then the representation \[{{S}_{1}},{{S}_{11}}\] with respect to point \[\left( {{x}_{1}},{{y}_{1}} \right)\] is given as
\[\Rightarrow {{S}_{1}}=y{{y}_{1}}-2a\left( x+{{x}_{1}} \right)\]
\[\Rightarrow {{S}_{11}}={{y}_{1}}^{2}-4a{{x}_{1}}\]
Now, by using the mid – point \[\left( h,1-h \right)\] to the curve \[S\equiv {{y}^{2}}-4ax=0\] we get the equation of chord as
\[\begin{align}
  & \Rightarrow {{S}_{1}}={{S}_{11}} \\
 & \Rightarrow y\left( 1-h \right)-2a\left( x+h \right)={{\left( 1-h \right)}^{2}}-4ah \\
 & \Rightarrow y\left( 1-h \right)-2ax={{\left( 1-h \right)}^{2}}-2ah \\
\end{align}\]
We are given that the chords are drawn from the point \[\left( a,2a \right)\] so, we can say that the point \[\left( a,2a \right)\] satisfies the above equation.
By substituting the point \[\left( a,2a \right)\] in above equation we get
\[\begin{align}
  & \Rightarrow 2a\left( 1-h \right)-2a\left( a \right)={{\left( 1-h \right)}^{2}}-2ah \\
 & \Rightarrow 2a-2{{a}^{2}}={{\left( 1-h \right)}^{2}} \\
\end{align}\]
We know that the square of any number is greater than 0. So, we can write
\[\Rightarrow {{\left( 1-h \right)}^{2}}>0\]
By substituting the required equation in above equation we get
\[\Rightarrow 2a-2{{a}^{2}}>0\]
Now, by multiplying with negative sign the inequality changes as
\[\begin{align}
  & \Rightarrow 2{{a}^{2}}-2a<0 \\
 & \Rightarrow 2a\left( a-1 \right)<0 \\
 & \Rightarrow a\in \left( 0,1 \right) \\
\end{align}\]
We know that the length of latus rectum of given parabola is \['4a'\]
Therefore the range of latus rectum can be taken as
\[\Rightarrow 4a\in \left( 0,4 \right)\]
Here, we can say that the length of latus rectum can take any values in the domain \[\left( 0,4 \right)\]
Therefore, the possible values of latus rectum according to options are 1, 2. So, option (a) and option (b) are correct answers.

Note: Students may make mistakes in solving the inequality. While multiplying with a negative sign the inequality changes. Here, we have
\[\Rightarrow 2a-2{{a}^{2}}>0\]
After multiplying with a negative sign the equation changes as
\[\Rightarrow 2{{a}^{2}}-2a<0\]
But students miss this point and do not change the inequality which results in wrong answers.
Also, we have the range of latus rectum as
\[\Rightarrow 4a\in \left( 0,4 \right)\]
This means the latus rectum can have values in the domain \[\left( 0,4 \right)\] but will not equal to ‘0’ or ‘4’. Students may miss this point and give the answer ‘4’ also as the correct answer. This will be wrong.