Question

If two distinct chords, drawn from the point \[\left( {p,q} \right)\] on the circle \[{x^2} + {y^2} = px + qy\]. Given that: \[pq \ne 0\] are bisected by the x-axis, then
A. \[{p^2} < 8{q^2}\]
B. \[{p^2} > 8{q^2}\]
C. Cannot be determined
D. None of these

Answer 1

Hint: The given problem revolves around the concepts of geometry. Keeping in mind, first of all, drawing the rough figure/construction from the given data; finding the coordinates of the other end of the respective distinct chord (using the midpoint formula, \[\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\]). As a result, consider the given equation of the circle i.e. \[{x^2} + {y^2} = px + qy\] and then substitute the coordinates in that equation. Then, by the condition given i.e. \[pq \ne 0\], using the condition of discrimination such as \[{b^2} - 4ac > 0\], etc., the desire solution is obtained.

Complete step by step answer:

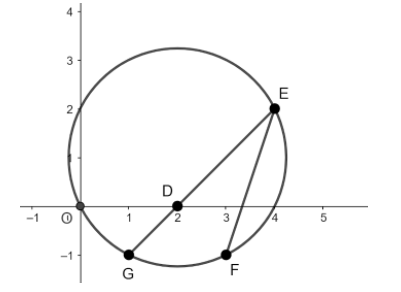
Let us assume the rough figure as drawn above from the respective given data which seems that,
\[E \equiv \left( {p,q} \right) \equiv \left( {{x_1},{y_1}} \right)\]
As we have given that it exists two distinct chords that is ‘\[{\text{EG}}\]’ and ‘\[{\text{EF}}\]’ in the above figure,
Hence, from the construction of the figure it is observed that point ‘\[{\text{D}}\]’ is the midpoint of the chord ‘\[{\text{EG}}\]’ as it bisects the \[x\]-axis,
So,
Let us consider the coordinates of point ‘\[{\text{D}}\]’ as,
\[D \equiv \left( {g,0} \right)\]
Where, ‘\[g\]’ is the coordinate due to on \[x\]-axis i.e. \[x = g\], and
‘\[0\]’ no point exists on \[y\]-axis i.e. \[y = 0\].
Hence, we can now find the coordinates of point ‘\[{\text{G}}\]’ from the midpoint formula i.e. \[\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\] as ‘\[{\text{D}}\]’ is the midpoint of ‘\[{\text{EG}}\]’, we get
\[ \Rightarrow \left( {g,0} \right) = \left( {\dfrac{{p + {x_2}}}{2},\dfrac{{q + {y_2}}}{2}} \right)\] … (Where, \[{x_2},{y_2}\] are the coordinates of point ‘\[{\text{G}}\]’)
Now, equating the equation \[x\]-coordinates mathematically, that is
\[g = \dfrac{{p + {x_2}}}{2}\]
\[2g = p + {x_2}\]
Hence, \[{x_2} = 2g - p\]
Similarly,
Equating the \[y\]-coordinates, we get
\[0 = \dfrac{{q + {y_2}}}{2}\]
\[0 = q + {y_2}\]
Hence, \[{y_2} = - q\]
The coordinates of point ‘\[{\text{G}}\]’ on chord ‘\[{\text{EG}}\]’ is,
\[G \equiv \left( {2g - p, - q} \right)\]
Now,
Since, considering the given equation (of the circle)
\[ \Rightarrow {x^2} + {y^2} = px + qy\]
Hence, as the point ‘\[{\text{G}}\]’ exists from these distinct point i.e. \[\left( {p,q} \right)\]
Substituting the values of \[x = {x_2} = 2g - p\] and \[y = {y_2} = - q\] in the equation as the coordinates i.e. \[{x_1} = p\] and \[{y_1} = q\], we get
\[ \Rightarrow {\left( {2g - p} \right)^2} + {\left( { - q} \right)^2} = p\left( {2g - p} \right) + q\left( { - q} \right)\]
Solving the equation algebraically, we get
\[ \Rightarrow 4{g^2} - 4gp + {p^2} + {q^2} = 2pg - {p^2} - {q^2}\] … [\[\because {\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\]]
\[ \Rightarrow 4{g^2} - 4gp + {p^2} + {q^2} - 2pg + {p^2} + {q^2} = 0\]
Simplifying the equation, we get
\[ \Rightarrow 4{g^2} - 6pg + 2\left( {{p^2} + {q^2}} \right) = 0\]
\[ \Rightarrow 2{g^2} - 3pg + \left( {{p^2} + {q^2}} \right) = 0\] … (i)
Since, given that \[pq \ne 0\] which seems to be real that is they are the coordinates
Hence, considering ‘\[g\]’ as the variable in the above equation
We know that the discriminant for real numbers is,
\[ \Rightarrow {b^2} - 4ac > 0\]
Hence, substituting the values from the equation (i), we get
\[{\left( { - 3p} \right)^2} - 4 \times 2 \times \left( {{p^2} + {q^2}} \right) > 0\]
\[9{p^2} - 8\left( {{p^2} + {q^2}} \right) > 0\]
Solving the equation predominantly, we get
\[9{p^2} - 8{p^2} - 8{q^2} > 0\]
\[{p^2} - 8{q^2} > 0\]
Hence, the required solution is
\[ \Rightarrow {p^2} > 8{q^2}\]

So, the correct answer is “Option B”.

Note:
 The given problem can be solved similarly by considering any one of the distinct chords (among two) by the same coordinates given i.e. \[\left( {p,q} \right)\]. One must able to know all the discrimination conditions that is \[{b^2} - 4ac > 0\], \[{b^2} - 4ac < 0\], \[{b^2} - 4ac = 0\] which seems the condition for real, imaginary and the exact solution respectively, so as to be sure of our final answer.