Question

If two circles intersect at two points, then prove that their centres lie on the perpendicular bisector of the common chord.

Answer 1

Hint: First draw 2 circles such that they intersect at two points then join the intersecting points and point of centre. Then use congruence of triangles to proceed.

Complete step by step answer:

In the question we are given that if two circles intersect at two points, then we have to prove that their centres lie on the perpendicular bisector of the common chord.
Now, let’s draw two circles with centres O and P such that they intersect each other at two distinct points let’s say A and B.
Now we will join points A and B so that AB is a common chord for both circles and then join OP.
Now we will use axioms of congruence.
Let’s consider two triangles OAP, OBP we see that $OA=OB$ as they are the radius of some circle.
Also $AP=BP$ as they are the radius of the same circle.
And finally $OP=OP$ as it is a common side of triangle OAP and OBP.
So, $\therefore \Delta OAP\cong \Delta OBP$ by the side-side-side axiom of congruency.

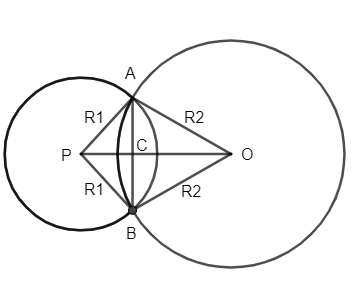
As we know that triangles OAP and OBP are congruent to each other. So, we can say that,
$\angle AOP=\angle BOP$
And $\angle AOC=\angle BOC$ ………………………………………….(i)
by saying congruent parts of congruent triangles.
Now, we will consider two triangles AOC and BOC,
We can see that $OA=OB$ as they are the same radii of the same circle.
From (i), we can say that $\angle AOC=\angle BOC$. And $OC=OC$ as it is the common side of both triangles.
So, $\therefore \Delta AOC\cong \Delta BOC$
As we know that triangles AOC and BOC is congruent to each other so, we can say that
$\angle ACO=\angle BCO$ and $AC=BC$ by saying congruent parts of congruent triangles.
But as we know that, $\angle ACO+\angle BCO=180{}^\circ $
So, $\angle ACO=\angle BCO=90{}^\circ $
Thus, OP is the perpendicular bisector of AB.
Hence, proved.

Note: Students should know the properties of circles and triangles. They should also know the axioms of congruence.