Question

If two adjacent angles are supplementary, prove that they form a linear pair.

Answer 1

Hint: In this question, we have to prove that a linear pair is formed if two adjacent angles are supplementary. We can use the properties of adjacent angles, supplementary angles and linear pairs to prove.

Complete step-by-step answer:
Before proving, we need to understand the meaning of adjacent angles, supplementary angles and linear pairs.
Adjacent angles are those angles that have a common arm and a common vertex. For example, in this figure, $\angle AOB$ and $\angle AOC$ are adjacent angles as they have a common arm- arm AO, and a common vertex- vertex O.

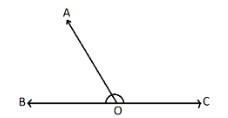
Supplementary angles are those pairs of angles which add up to $180^\circ $. It is not necessarily required for the angles to be adjacent. For example, any two angles measuring $113^\circ $ and $67^\circ $are supplementary.
On the other hand, a linear pair of angles add up to $180^\circ $and are formed by two adjacent angles. The two angles also make up a straight line.
 

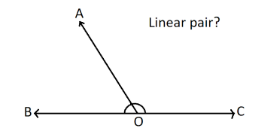
In the above figure, $\angle AOB$ and $\angle AOC$ are adjacent angles as they have a common arm AO and a common vertex O. Also, we can notice that the sum of the two angles is $180^\circ $. Hence, the two angles are supplementary. In addition to this, it can also be observed that the two angles together lie on a straight line which proves that they form a linear pair.

Therefore, if the two angles are supplementary, they form a linear pair.

Note: The student must not think that supplementary angles and linear pair are one and the same thing. For two angles to be supplementary, it is not necessary that they should be adjacent as well. However, for two angles to be considered as a linear pair, it is necessary for them to be adjacent.