Question

If three cubes of metal whose edges are 30 cm, 40 cm and 50 cm respectively are melted and formed into a single cube, the total surface area of the single new cube is
\[\left( a \right)2.0{{m}^{2}}\]
\[\left( b \right)2.15{{m}^{2}}\]
\[\left( c \right)2.16{{m}^{2}}\]
\[\left( d \right)2.2{{m}^{2}}\]

Answer 1

Hint: We are given three cubes, we need to melt them to make a new cube. When we recast the cube, the volume is always fixed. So, we use volume to find the dimension of the new cube. Once, we have the dimension, we can find the surface area. The volume is given by \[{{s}^{3}},\] where s is the side of the cube and the surface area by \[6{{s}^{2}}.\]

Complete step-by-step answer:

We are given that we have 3 cubes of sides 30 cm, 40 cm, and 50 cm respectively. We know that the volume of the objects is always the same before and after melting.

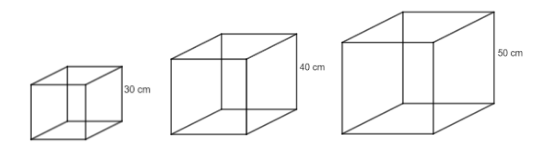
So,
The volume of New Cube = Volume of Three Cubes
Let s be the side of the new cube, so
\[V=\text{Volume of new cube}=s\times s\times s={{s}^{3}}\]
Now,
\[{{V}_{1}}=\text{Volume of cube with side 30cm}=30\times 30\times 30=27000c{{m}^{3}}\]
\[{{V}_{2}}=\text{Volume of cube with side 40cm}=40\times 40\times 40=64000c{{m}^{3}}\]
\[{{V}_{3}}=\text{Volume of cube with side 50cm}=50\times 50\times 50=125000c{{m}^{3}}\]
So,
\[V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}\]
\[\Rightarrow {{s}^{3}}=27000+64000+125000\]
\[\Rightarrow {{s}^{3}}=216000\]
\[\Rightarrow s=\sqrt[3]{216000}\]
\[\Rightarrow s=60cm\]
We got the side of the new cube as 60 cm.
Now, we will find the surface area of the cube. The surface area of the cube is given as
\[\text{Total Surface Area}=6{{s}^{2}}\]
We know that side is 60cm, so we get,
\[\text{Total Surface Area}=6\times 60\times 60=21600c{{m}^{2}}\]
So, we get the surface area as \[21600c{{m}^{2}}.\]
Now, we need the solution in \[{{m}^{2}},\] so we will convert the answer to \[{{m}^{2}}.\]
We know that,
\[1{{m}^{2}}=10000c{{m}^{2}}\]
Or
\[10000c{{m}^{2}}=1{{m}^{2}}\]
So, we get,
\[1c{{m}^{2}}=\dfrac{1}{10000}{{m}^{2}}\]
Therefore,
\[21600c{{m}^{2}}=\dfrac{1}{10000}\times 21600{{m}^{2}}\]
\[\Rightarrow 2.16{{m}^{2}}\]
Therefore we get the surface area as \[2.16{{m}^{2}}.\]
So, the correct answer is “Option C”.

Note: Students while solving should keep in mind to convert the answer into the correct form, i.e. \[{{m}^{2}}\] to \[c{{m}^{2}}\] in this case. While adding or multiplying complex numbers, always cross-check your answer as a small mistake can lead to a big error at the end of the solution. Students may compute \[LSA=4{{s}^{2}}\] instead of \[TSA=6{{s}^{2}}\] and get the wrong answer. Here, LSA stands for Lateral Surface Area and TSA stands for Total Surface Area.