Question

If $\theta $ and $\left( {2\theta - 45} \right)$ are acute angles and $\sin \theta = \cos \left( {2\theta - 45} \right)$ then $\tan \theta = .....$

Answer 1

Hint: The angles whose measurement results as less than the 90 degrees then, it is known as an Acute angle while at the same time, the angles whose measurement results as more than the 90 degrees then, it is known as an Obtuse angle. Angles measuring 90 degrees exactly is known as right-angles.
One of the properties of the triangles which needs to be followed here is that the sum of the interior angles of the triangle is 180 degrees.
Here, in the question, we need to determine the value of \[\theta \] and then, consequently, the value of $\tan \theta $ for which, first of all, calculate the value of $\theta $ and then evaluate the corresponding value of $\tan \theta $.

Complete answer:
From the given figure:

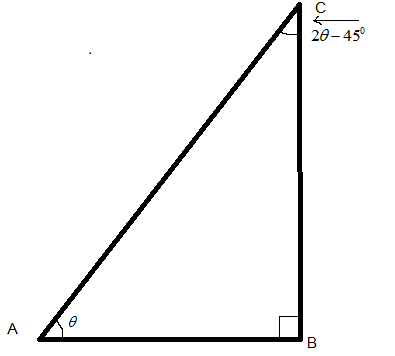
$\angle CAB = \theta ,\angle CBA = {90^0},\angle BCA = \left( {2\theta - {{45}^0}} \right)$
Following the property of the triangle that the sum of the angles of the triangle is ${180^0}$. So adding all the interior angles of the triangle ABC as:
$\angle CAB + \angle CBA + \angle BCA = {180^0} \\
\theta + {90^0} + \left( {2\theta - 45} \right) = {180^0} \\
3\theta = {180^0} - {90^0} + {45^0} \\
3\theta = {135^0} \\
\theta = \dfrac{{{{135}^0}}}{3} = {45^0} \\$
Now, substituting the value of $\theta $ in the given equation of the question $\sin \theta = \cos \left( {2\theta - 45} \right)$ and check whether this value of $\theta $ is satisfying the condition of the question or not.
$\sin \theta = \cos \left( {2\theta - 45^0} \right) \\
\sin 45^0 = \cos (2 \times 45^0 - 45) \\
\sin 45^0 = \cos 45^0 \\
\dfrac{1}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} \\$
Hence, it can be seen that the calculated value of $\theta $ is satisfying the condition.
Now, substitute $\theta = 45^0$ in the function $\tan \theta $ to determine the value.
$\tan \theta = \tan 45^0 \\
= 1 \\$
Hence, the value of $\tan \theta $ at $\theta = {45^0}$ is 1.

Note: Alternatively, this question can also be done by using trigonometric identities as:
$\sin \theta = \cos \left( {2\theta - 45} \right) \\
\cos \left( {\dfrac{\pi }{2} - \theta } \right) = \cos \left( {2\theta - 45} \right) \\
90 - \theta = 2\theta - 45 \\
3\theta = 135 \\
\theta = \dfrac{{135}}{3} = 45 \\$
Here also, the value of $\theta $ comes out to be 45 degrees and so the value of corresponding $\tan \theta $ can be calculated as: $\tan 45 = 1$.