Question

If , then find the value of :
A.\[\dfrac{{\sqrt {1 - {a^2} + a} }}{{\sqrt {1 - {a^2}} }}\]
B.\[\dfrac{{\sqrt {1 - {a^2} + 1} }}{{\sqrt {1 - {a^2}} }}\]
C.\[\dfrac{{a(\sqrt {1 - {a^2}} \, + \,1)}}{{\sqrt {1 - {a^2}} }}\]
D.\[\dfrac{{1 + \sqrt {1 - {a^2}} }}{{\sqrt {1 - {a^2}} }}\]

Answer 1

Hint: First, we have to define what the terms we need to solve the problem are.Each degree is then further divided into \[60\] minutes denoted by ‘, for example
\[{10^ \circ }6'\]
Each minute is then further divided into \[60\] seconds denoted by “, for example
This can be pronounced as “Ten degrees six minutes thirty-two seconds”
Here we are given
To find the required answer, we need to find cos and tan in terms of a using

Formula to be used:

\[\sin ({90^ \circ } - \theta ) = \cos \theta \]
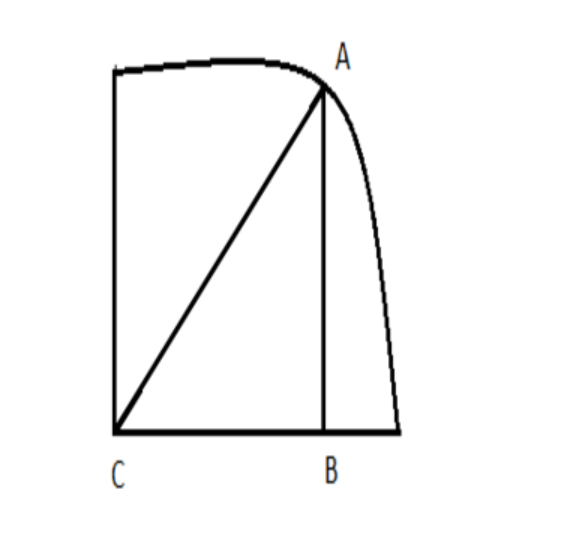
According to Pythagoras theorem
\[A{B^2} + B{C^2} = A{C^2}\]
\[AC = \]hypotenuse
\[AB = \]perpendicular
\[BC = \]base
In trigonometry,
Let \[\angle ACB = \theta \]
\[{\sin ^2}\theta + {\cos ^2}\theta = 1\]
\[\sin \theta = \dfrac{{Perpendicular}}{{Hypotenuse}}\]
\[\cos \theta = \dfrac{{Base}}{{Hypotenuse}}\]
\[\tan \theta = \dfrac{{Perpendicular}}{{Base}}\]
\[\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}\]

Complete answer:
It is given that
 =\[\dfrac{{Perpendicular}}{{Hypotenuse}}\]
Since,
\[AC = \]hypotenuse
\[AB = \]perpendicular
\[BC = \]base
And,
\[A{B^2} + B{C^2} = A{C^2}\]
We can find the value of the base with this equation and place all the values:
\[B{C^2} = A{C^2} - A{B^2}\]
\[BC = \sqrt {A{C^2} - A{B^2}} \]
\[BC = \sqrt {1 - {a^2}} \]
So the base is \[\sqrt {1 - {a^2}} \]
Now we can find cos value for that same angle \[\theta \], by applying the Pythagoras theorem for trigonometric identities
Since we know, the value of both sin and cos
\[\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}\]
So, to find the value of \[\tan \theta \]
And also,
\[\sin ({90^ \circ } - \theta ) = \cos \theta \]
Make sure that the value of minute and second do not exceed $60$.
Now we know the value of and
So adding both we get

Hence, the correct option is (C) \[\dfrac{{a(\sqrt {1 - {a^2}} \, + \,1)}}{{\sqrt {1 - {a^2}} }}\]

Note:
Using the given , we need to apply the Pythagoras theorem. Applying the theorem, we are able to find the value of the base, the perpendicular, and the hypotenuse.
The concept of angle: A circle is divided into \[360\] equal parts. It is known as the degree where there is a sign of negative sign and a degree greater than \[360\] in degree used in trigonometric terms, it is one of the measurement units in angle.