Question

If the width of a hollow cylinder is 2 cm. Its internal diameter is 14 cm and height 26 cm. The two ends of the cylinder are opened. Find the total surface area of the hollow cylinder.

Answer 1

Hint: Here the question is related to the mensuration topic. We have to determine the total surface of the hollow cylinder. This can be determined by using the formula \[T.S.A = 2\pi ({r_1} + {r_2})({r_1} - {r_2} + h)\], where \[{r_1}\,and\,{r_2}\] represents the external and internal radius a cylinder respectively.

Complete step by step solution:
A hollow cylinder is made up of two thin sheets of rectangle having a length and breadth. Also, the radius of both the cylinders can be r1+r2. Therefore, the surface area of the cylinder is equal to the surface area of both the rectangles which is equal to \[2\pi ({r_1} + {r_2})({r_1} - {r_2} + h)\]
Now consider the given question

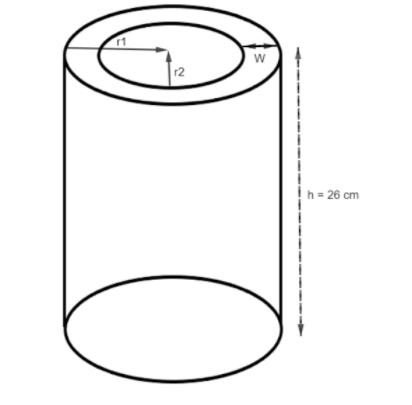
The width of a hollow cylinder = 2 cm.
The internal diameter of a hollow cylinder = 14 cm.
The internal radius of a hollow cylinder = \[\dfrac{{14}}{2}\, = \,7\]cm.
The internal radius of the hollow cylinder is represents as \[{r_2}\]
Therefore \[{r_2} = 7\,cm\]
Now we have to determine the radius of the hollow cylinder. So we have to add the internal radius and width.
So, we have
\[{r_1} = {r_2} + w\]
On adding we have
\[ \Rightarrow {r_1} = 7 + 2 = 9\,cm\]
Therefore, the external radius of hollow cylinder is represents \[{r_1}\] and its value is \[{r_1} = 9\,cm\]
The height of the hollow cylinder \[h = 26\,cm\]
The total surface area of a hollow cylinder is given by \[T.S.A = 2\pi ({r_1} + {r_2})({r_1} - {r_2} + h)\]
On substituting the values we have
\[ \Rightarrow T.S.A = 2\pi (9 + 7)(9 - 7 + 26)\]
On simplifying we have
\[ \Rightarrow T.S.A = 2\pi (16)(28)\]
Take \[\pi = \dfrac{{22}}{7}\], on substituting the value of pi
\[ \Rightarrow T.S.A = 2 \times \dfrac{{22}}{7} \times (16) \times (28)\]
On simplifying we have
\[ \Rightarrow T.S.A = 2816\,c{m^2}\]
Therefore, the total surface area of hollow cylinder is \[2816\,c{m^2}\]
So, the correct answer is “ \[2816\,c{m^2}\]”.

Note: The total surface area for the cylinder and hollow cylinder is different from each other. The total surface area of cylinder \[2\pi r(r + h)\]but the formula for the total surface area of hollow cylinder is \[2\pi ({r_1} + {r_2})({r_1} - {r_2} + h)\]. If it’s an area we have to mention the units. The unit for the area is square units.