Question

If the volume of a prism is $1920\sqrt{3}c{{m}^{3}}$and the side of the equilateral base is $16\text{ }cm$, then the height (in cm) of the prism is?
$\begin{align}
  & A.\text{ 19} \\
 & \text{B}\text{. 20} \\
 & \text{C}\text{. 30} \\
 & \text{D}\text{. 40} \\
\end{align}$

Answer 1

Hint: In the given question volume of a prism and side of the equilateral base is given and we have to find out the height of the prism. So first of all, we have to know about a prism. A prism is a solid whose top and bottom faces are parallel to each other and identical polygons. In the given question the polygon is an equilateral triangle. In a prism if a perpendicular is drawn from the centre of the top face, it passes through the centre of base.
Volume of a prism is equal to the base area multiplied by height of prism.
$V=AH$ where $A$is the base area and $H$ is the height of prism.

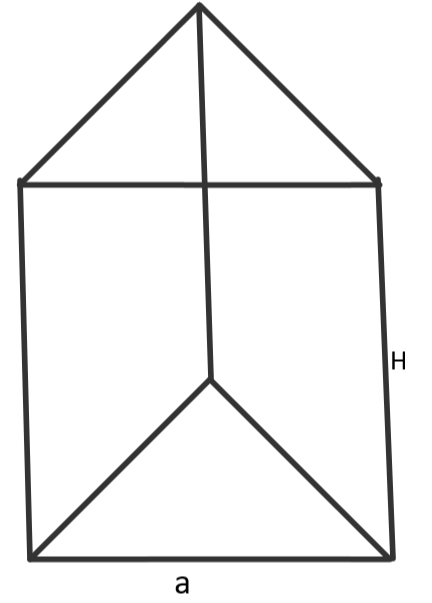
As base of prism is an equilateral triangle so its area can be calculated as
$A=\dfrac{\sqrt{3}}{4}{{a}^{2}}$ where $a$is side of equilateral triangle
So, first calculate the base area of the prism and then use the formula $V=AH$ in order to calculate the height of the prism.

Complete step-by-step answer:
It is given in question side of equilateral base $a=16cm$
So, area of equilateral triangle
$\begin{align}
  & A=\dfrac{\sqrt{3}}{4}{{a}^{2}} \\
 & A=\dfrac{\sqrt{3}}{4}{{\left( 16 \right)}^{2}} \\
\end{align}$
As we know that volume of prism
$V=AH$
It is given from question
$V=1920\sqrt{3}\text{ }c{{m}^{3}}$
Substituting the given value, we can write
$1920\sqrt{3}\text{ c}{{\text{m}}^{3}}\text{=}\dfrac{\sqrt{3}}{4}{{(16)}^{2}}(H)c{{m}^{2}}$
So, after rearranging we can write
$H=\dfrac{4(1920)(\sqrt{3})c{{m}^{3}}}{\left( \sqrt{3} \right){{(16)}^{2}}c{{m}^{2}}}$
Now we can cancel the common terms we can write
$\begin{align}
  & H=\dfrac{1920}{64}cm \\
 & H=30cm \\
\end{align}$
Hence the height of the prism is 30 cm. So, option C is correct.

Note: When we talk about prism it means a right prism in general. In such a prism the lateral face of the prism is perpendicular to the base. There are as many lateral faces as there are sides in the base.
Also, \[\text{Lateral Surface area}= \left( \text{Perimeter of base} \right) \left( \text{height of prism} \right)\]
\[\text{Total surface area }=\text{Lateral surface area} +2(\text{Area of base})\]