Question

If the vertices of a triangle are (1,-3), (4,p) and (-9,7) and its area is 15 sq. units, then find the value (s) of p.

Answer 1

Hint: The formula $ar\left( \Delta ABC \right)=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]$ for any three coordinates $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)$ of a triangle is used to find the value of p after substituting all the given values in the above-mentioned equation.

Complete step by step answer:
Let us consider a triangle ABC with the coordinates A (1, -3), B (4, p) and C (-9,7).

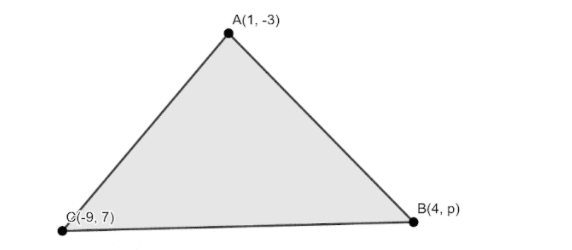
We know, the area of a triangle ABC with the three coordinates $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right),C\left( {{x}_{3}},{{y}_{3}} \right)$ is given by the numerical value of the expression
$ar\left( \Delta ABC \right)=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\ldots \left( i \right)$
Here,
$\begin{align}
  & \left( {{x}_{1}},{{y}_{1}} \right)=\left( 1,-3 \right) \\
 & \left( {{x}_{2}},{{y}_{2}} \right)=\left( 4,p \right) \\
 & \left( {{x}_{3}},{{y}_{3}} \right)=\left( -9,7 \right) \\
 & ar\left( \Delta ABC \right)=15 \\
\end{align}$
Substituting these values in equation (i), we get
$15=\dfrac{1}{2}\left[ 1\left( p-7 \right)+4\left( 7-(-3) \right)+-9\left( -3-p \right) \right]$
Solving this, we get
$\begin{align}
  & \text{ }\dfrac{1}{2}\left[ \left( p-7 \right)+4\left( 7+3 \right)-9\left( -3-p \right) \right]=15 \\
 & \Rightarrow p-7+40+27+9p=30 \\
 & \Rightarrow p+9p=30-27+7-40 \\
 & \Rightarrow 10p=-30 \\
 & \Rightarrow p=-3 \\
\end{align}$

Hence, the value of p is -3.

Note: We should use this formula and do the calculations with utmost care, because a single error will change the answer. Always double-check the formula and calculations after solving. We should keep in mind that area is a measure, that is, it cannot be negative. If the area of a triangle comes out zero, then it means that the three points are collinear points. The best way to remember this formula is to remember the cycle of 1, 2, 3.

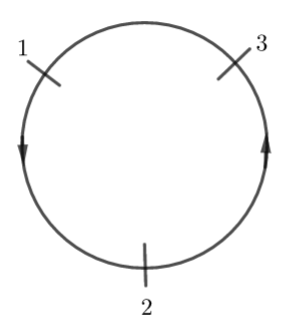
The cycle goes as 1, 2, 3 which means the first expression is ${{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)$.
Then the cycle moves to 2, 3, 1 which means the second expression is ${{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)$. Then the cycle moves further as 3, 2, 1 which means the third expression is ${{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right)$. Once we remember these three expressions correctly, then the rest of the formula can be easily remembered.