Question

If the vertex of the parabola is \[\left( 2,0 \right)\] and the extremities of the latus rectum are \[\left( 3,2 \right)\]and \[\left( 3,-2 \right)\] then the equation of the parabola is
\[\begin{align}
  & \text{A}\text{. }{{\text{y}}^{2}}=2x-4 \\
 & \text{B}\text{. }{{\text{x}}^{2}}=4y-8 \\
 & \text{C}\text{. }{{\text{y}}^{2}}=4x-8 \\
 & \text{D}\text{. None of these} \\
\end{align}\]

Answer 1

Hint: We know that if the latus rectum is perpendicular to y-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)\]. In the same way, if the latus rectum is perpendicular to x-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( x-{{x}_{1}} \right)}^{2}}=4a\left( y-{{y}_{1}} \right)\]. From the question, it is given that the vertex of the parabola is \[\left( 2,0 \right)\] and the extremities of the latus rectum are \[\left( 3,2 \right)\]and \[\left( 3,-2 \right)\]. So, we will find the equation of latus rectum. Then by using the above concept, we will find the equation of parabola.

Complete step-by-step answer:
Before solving the question, we should know that if the latus rectum is perpendicular to y-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)\]. In the same way, if the latus rectum is perpendicular to x-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( x-{{x}_{1}} \right)}^{2}}=4a\left( y-{{y}_{1}} \right)\].

From the question, it is given that the vertex of the parabola is \[\left( 2,0 \right)\] and the extremities of the latus rectum are \[\left( 3,2 \right)\]and \[\left( 3,-2 \right)\].

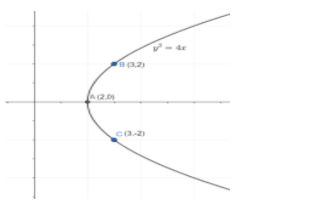
Now we have to find the equation of the latus rectum.
We know that if \[A\left( {{x}_{1}},{{y}_{1}} \right)\] and \[B\left( {{x}_{2}},{{y}_{2}} \right)\] are two points, then the line passing through \[A\left( {{x}_{1}},{{y}_{1}} \right)\] and \[B\left( {{x}_{2}},{{y}_{2}} \right)\] is \[y-{{y}_{1}}=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)\].
Now we have to find the equation of line passing through \[\left( 3,2 \right)\]and \[\left( 3,-2 \right)\].
\[\begin{align}
  & y-2=\dfrac{-2-2}{3-3}\left( x-3 \right) \\
 & \Rightarrow y-2=\dfrac{-4}{0}\left( x-3 \right) \\
 & \Rightarrow x=3 \\
\end{align}\]
We know that a line \[x=k\] is perpendicular to the y-axis. Hence, we can say that the latus rectum is perpendicular to y-axis.
We should know that if the latus rectum is perpendicular to y-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)\].
So, the equation of parabola whose vertex is \[\left( 2,0 \right)\] is
\[\begin{align}
  & {{\left( y-0 \right)}^{2}}=4a\left( x-2 \right) \\
 & \Rightarrow {{y}^{2}}=4a\left( x-2 \right).....(1) \\
\end{align}\]
We know that the extremities of the latus rectum passes through the parabola. So, we can say that \[\left( 3,2 \right)\]and \[\left( 3,-2 \right)\] lie on equation (1).
So, let us substitute \[\left( 3,2 \right)\] in equation (1).
\[\begin{align}
  & \Rightarrow {{\left( 2 \right)}^{2}}=4a\left( 3-2 \right) \\
 & \Rightarrow 4=4\left( a \right) \\
 & \Rightarrow a=1....(2) \\
\end{align}\]
Now let us substitute equation (2) in equation (1), then we get
\[\begin{align}
  & \Rightarrow {{y}^{2}}=4\left( x-2 \right) \\
 & \Rightarrow {{y}^{2}}=4x-8 \\
\end{align}\]

So, the correct answer is “Option C”.

Note: Students may have a misconception that if the latus rectum is perpendicular to x-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( y-{{y}_{1}} \right)}^{2}}=4a\left( x-{{x}_{1}} \right)\]. In the same way, if the latus rectum is perpendicular to y-axis and the vertex of parabola is \[\left( {{x}_{1}},{{y}_{1}} \right)\], then the equation of the parabola is \[{{\left( x-{{x}_{1}} \right)}^{2}}=4a\left( y-{{y}_{1}} \right)\]. To avoid this conception, students should draw the graph of the parabola. By observing the graph, students may have a clear view.